1. What is the NTC Thermistor Temperature Calculator?

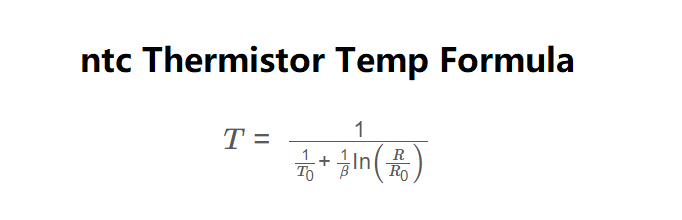
Definition: This calculator determines the temperature corresponding to a measured resistance of an NTC (Negative Temperature Coefficient) thermistor, using the thermistor's nominal resistance, reference temperature, and beta value. NTC thermistors decrease in resistance as temperature increases.

Purpose: Engineers, technicians, and hobbyists use this tool to interpret temperature readings from NTC thermistors in applications like temperature sensors, HVAC systems, medical devices, and automotive electronics.

2. How Does the Calculator Work?

The calculator uses the rearranged beta equation, as shown in the image above:

\( T = \frac{1}{\frac{1}{T_0} + \frac{1}{\beta} \ln\left(\frac{R}{R_0}\right)} \)

Where:

• \( T \): Temperature at measured resistance \( R \) (in Kelvin);
• \( R \): Measured resistance;
• \( R_0 \): Nominal resistance at reference temperature \( T_0 \);
• \( \beta \): Beta value, a material constant (in Kelvin);
• \( T_0 \): Reference temperature (in Kelvin).

Steps:

• Enter the nominal resistance (\( R_0 \)) at reference temperature \( T_0 \), and select its unit (Ω, kΩ, MΩ).
• Enter the reference temperature (\( T_0 \)) and select its unit (°C or °F); defaults to 25°C.
• Enter the beta value (\( \beta \)) in Kelvin.
• Enter the measured resistance (\( R \)) and select its unit (Ω, kΩ, MΩ).
• Select the output temperature unit (°C or °F).
• The calculator converts resistances to ohms, temperatures to Kelvin, and computes \( T \) using the rearranged beta equation.
• The result is converted to the selected temperature unit, formatted (scientific notation for values < 0.001, otherwise 4 decimal places), and displayed.

3. Importance of NTC Thermistor Temperature Calculation

Calculating temperature from thermistor resistance is critical for:

• Temperature Monitoring: Converts resistance readings to accurate temperature values in real-time monitoring systems.
• System Calibration: Allows calibration of temperature sensors in electronics for specific operating conditions.
• Diagnostics: Helps diagnose temperature-related issues in devices by interpreting thermistor data.

4. Using the Calculator

Example 1: Calculate the temperature for an NTC thermistor with \( R_0 = 10 \, \text{kΩ} \) at \( T_0 = 25 \, \text{°C} \), \( \beta = 3950 \, \text{K} \), and measured resistance \( R = 5.9826 \, \text{kΩ} \), outputting in °C:

• \( R_0 \): 10 kΩ = 10000 Ω;
• \( R \): 5.9826 kΩ = 5982.6 Ω;
• \( T_0 \): 25°C = 298.15 K;
• \( \ln\left(\frac{R}{R_0}\right) \): \( \ln\left(\frac{5982.6}{10000}\right) \approx -0.5145 \);
• \( \frac{1}{T} \): \( \frac{1}{298.15} + \frac{1}{3950} \cdot (-0.5145) \approx 0.003094 \);
• \( T \): \( \frac{1}{0.003094} \approx 323.15 \, \text{K} = 50.00 \, \text{°C} \).

Example 2: Calculate the temperature for an NTC thermistor with \( R_0 = 10000 \, \text{Ω} \) at \( T_0 = 77 \, \text{°F} \), \( \beta = 3435 \, \text{K} \), and measured resistance \( R = 0.0136906 \, \text{MΩ} \), outputting in °F:

• \( R_0 \): 10000 Ω;
• \( R \): 0.0136906 MΩ = 13690.6 Ω;
• \( T_0 \): 77°F = 25°C = 298.15 K;
• \( \ln\left(\frac{13690.6}{10000}\right) \approx 0.3142 \);
• \( \frac{1}{T} \): \( \frac{1}{298.15} + \frac{1}{3435} \cdot 0.3142 \approx 0.003663 \);
• \( T \): \( \frac{1}{0.003663} \approx 273.15 \, \text{K} = 0.00 \, \text{°C} = 32.00 \, \text{°F} \).

5. Frequently Asked Questions (FAQ)

Q: How accurate is the beta equation for temperature calculation?
A: The beta equation is an approximation and is most accurate over a narrow temperature range. For higher precision across a wider range, the Steinhart-Hart equation may be preferred.

Q: Why can I select different units for \( R_0 \) and \( R \)?
A: Independent unit selection allows flexibility when measuring resistance with different tools or in different contexts (e.g., \( R_0 \) in kΩ from a datasheet, \( R \) in Ω from a multimeter).

Q: What does it mean if the measured resistance is higher than the nominal resistance?
A: For an NTC thermistor, a higher resistance indicates a lower temperature than the reference temperature, since resistance decreases as temperature increases.

NTC Thermistor Temperature Calculator© - All Rights Reserved 2025