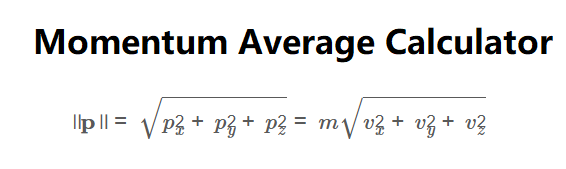Momentum Calculator – Momentum Average Calculator

Object 1

Mass (m):

Velocity X (v_x):

Velocity Y (v_y):

Velocity Z (v_z):

1. What is a Momentum Calculator – Momentum Average Calculator?

Definition: This calculator determines the linear momentum of an object given its mass and velocity components, as well as the average momentum for multiple objects.

Purpose: It is used in physics to analyze the momentum of moving objects, such as in collisions or multi-object systems, aiding in understanding conservation of momentum principles.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Momentum Components: \[ p_x = m v_x, \quad p_y = m v_y, \quad p_z = m v_z \] Total Momentum Magnitude: \[ \|\mathbf{p}\| = \sqrt{p_x^2 + p_y^2 + p_z^2} = m \sqrt{v_x^2 + v_y^2 + v_z^2} \] Average Momentum (for multiple objects): \[ \mathbf{p}_{avg} = \frac{\sum \mathbf{p}_i}{n}, \quad \|\mathbf{p}_{avg}\| = \sqrt{(p_{avg,x})^2 + (p_{avg,y})^2 + (p_{avg,z})^2} \] Where:

\( p_x, p_y, p_z \): Momentum components (N·s)
\( \|\mathbf{p}\| \): Total momentum magnitude (N·s)
\( m \): Mass (mg, g, kg, oz, lb)
\( v_x, v_y, v_z \): Velocity components (m/s, km/h, ft/s, mph, kn, ft/min)
\( n \): Number of objects

Unit Conversions:

Mass Units (m): mg, g, kg, oz, lb
Velocity Units (v_x, v_y, v_z): m/s, km/h, ft/s, mph, kn, ft/min

Steps:

Enter the mass (m) for each object, selecting the unit (mg, g, kg, oz, lb)
Enter the velocity components (v_x, v_y, v_z) for each object, selecting the unit (m/s, km/h, ft/s, mph, kn, ft/min)
Add or delete objects as needed
Convert all inputs to SI units (kg, m/s)
Calculate the momentum components and total magnitude for each object
If multiple objects, calculate the average momentum components and magnitude
View the results in N·s

3. Importance of Momentum Calculation

Calculating momentum is crucial for:

Physics Education: Understanding the concept of momentum and its conservation in collisions.
Engineering and Safety: Analyzing the impact of moving objects in systems like vehicles or machinery.
Sports: Studying the motion of athletes or equipment, such as a ball in flight.

4. Using the Calculator

Examples:

Example 1: For an object with mass \( m = 2 \, \text{kg} \), velocity components \( v_x = 3 \, \text{m/s} \), \( v_y = 4 \, \text{m/s} \), \( v_z = 0 \, \text{m/s} \):
- \( p_x = 2 \times 3 = 6.000 \, \text{N·s} \)
- \( p_y = 2 \times 4 = 8.000 \, \text{N·s} \)
- \( p_z = 2 \times 0 = 0.000 \, \text{N·s} \)
- Total momentum = \( 2 \times \sqrt{3^2 + 4^2 + 0^2} = 2 \times 5 = 10.000 \, \text{N·s} \)
Example 2: For two objects:
- Object 1: \( m = 1 \, \text{lb} \), \( v_x = 10 \, \text{mph} \), \( v_y = 0 \, \text{mph} \), \( v_z = 0 \, \text{mph} \)
- Mass in kg = \( 1 \times 0.453592 = 0.453592 \, \text{kg} \)
- Velocity in m/s = \( 10 \times 0.44704 = 4.4704 \, \text{m/s} \)
- \( p_x = 0.453592 \times 4.4704 = 2.027 \, \text{N·s} \)
- \( p_y = 0, \quad p_z = 0 \)
- Total momentum = \( 2.027 \, \text{N·s} \)
- Object 2: \( m = 2 \, \text{lb} \), \( v_x = -5 \, \text{mph} \), \( v_y = 5 \, \text{mph} \), \( v_z = 0 \, \text{mph} \)
- Mass in kg = \( 2 \times 0.453592 = 0.907184 \, \text{kg} \)
- Velocity in m/s = \( 5 \times 0.44704 = 2.2352 \, \text{m/s} \)
- \( p_x = 0.907184 \times (-2.2352) = -2.027 \, \text{N·s} \)
- \( p_y = 0.907184 \times 2.2352 = 2.027 \, \text{N·s} \)
- \( p_z = 0 \)
- Total momentum = \( 0.907184 \times \sqrt{(-2.2352)^2 + (2.2352)^2 + 0^2} = 2.866 \, \text{N·s} \)
- Average: \( p_{avg,x} = \frac{2.027 - 2.027}{2} = 0.000 \, \text{N·s} \)
- \( p_{avg,y} = \frac{0 + 2.027}{2} = 1.014 \, \text{N·s} \)
- \( p_{avg,z} = 0 \)
- Average total momentum = \( \sqrt{0^2 + (1.014)^2 + 0^2} = 1.014 \, \text{N·s} \)

5. Frequently Asked Questions (FAQ)

Q: What is momentum?
A: Momentum (\( \mathbf{p} \)) is the product of an object's mass and velocity, calculated as \( \mathbf{p} = m \mathbf{v} \), and is a measure of how difficult it is to stop a moving object.

Q: Why calculate momentum components?
A: Momentum is a vector quantity, and its components (\( p_x, p_y, p_z \)) allow us to analyze motion in different directions, useful in 3D motion or collision problems.

Q: What is the average momentum?
A: The average momentum for multiple objects is the sum of their momentum vectors divided by the number of objects, useful for systems with multiple moving parts.