1. What is a Moment of Inertia Calculator?

Definition: This calculator computes the moment of inertia (\( I \)) of a rotating object about a specified axis, based on its shape, mass, dimensions, and axis of rotation.

Purpose: It is used in physics and engineering to analyze rotational motion, helping to understand how mass distribution affects an object's resistance to angular acceleration.

2. How Does the Calculator Work?

The calculator uses the following formulas for different shapes:

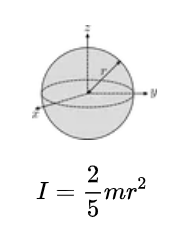
Ball (Solid): \[ I = \frac{2}{5} m r^2 \quad (\text{axis through center}) \] Circular Hoop (Thin): \[ I_z = m r^2 \quad (\text{axis parallel to z}) \] \[ I_x = I_y = \frac{1}{2} m r^2 \quad (\text{axis parallel to x or y}) \] Cuboid (Solid): \[ I_l = \frac{1}{12} m (w^2 + h^2) \quad (\text{axis parallel to length } l) \] \[ I_w = \frac{1}{12} m (l^2 + h^2) \quad (\text{axis parallel to width } w) \] \[ I_h = \frac{1}{12} m (l^2 + w^2) \quad (\text{axis parallel to height } h) \] \[ I_d = \frac{1}{6} m \frac{w^2 h^2 + l^2 h^2 + l^2 w^2}{l^2 + w^2 + h^2} \quad (\text{axis along longest diagonal } d) \] Cylinder (Solid): \[ I_z = \frac{1}{2} m r^2 \quad (\text{axis parallel to z}) \] \[ I_x = I_y = \frac{1}{12} m (3 r^2 + h^2) \quad (\text{axis parallel to x or y}) \] Cylindrical Tube: \[ I_z = \frac{1}{2} m (r_2^2 + r_1^2) \quad (\text{axis parallel to z}) \] \[ I_x = I_y = \frac{1}{12} m (3 (r_2^2 + r_1^2) + h^2) \quad (\text{axis parallel to x or y}) \] Where:

• \( I \): Moment of inertia (kg·m², kg·cm², g·cm²)
• \( m \): Mass (mg, g, dag, kg, oz, lb, st)
• \( r \): Radius (mm, cm, m, in, ft, yd)
• \( r_1 \): Inner radius (for tube) (mm, cm, m, in, ft, yd)
• \( r_2 \): Outer radius (for tube) (mm, cm, m, in, ft, yd)
• \( l \): Length (mm, cm, m, in, ft, yd)
• \( w \): Width (mm, cm, m, in, ft, yd)
• \( h \): Height (mm, cm, m, in, ft, yd)

Unit Conversions:

• Mass (\( m \)): mg (1 mg = 0.000001 kg), g (1 g = 0.001 kg), dag (1 dag = 0.01 kg), kg, oz (1 oz = 0.028349523125 kg), lb (1 lb = 0.45359237 kg), st (1 st = 6.35029318 kg)
• Length (\( r, r_1, l, w, h \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
• Moment of Inertia (\( I \)): kg·m², kg·cm² (1 kg·m² = 10000 kg·cm²), g·cm² (1 kg·m² = 100000 g·cm²)

Steps:

• Select the shape and axis of rotation.
• The corresponding image of the shape will be displayed.
• Enter the mass and dimensions (e.g., radius, length, width, height), and select their units.
• Convert all inputs to base units (kg for mass, m for lengths).
• Calculate the moment of inertia using the appropriate formula.
• Convert the result to the selected unit.
• Display the result, using scientific notation for values less than 0.001, otherwise with 3 decimal places.

3. Importance of Moment of Inertia Calculation

Calculating the moment of inertia is crucial for:

• Physics Education: Understanding rotational dynamics and angular momentum.
• Engineering Design: Designing rotating machinery, such as flywheels, gears, and turbines.
• Structural Analysis: Analyzing the stability and motion of structures under rotational forces.

4. Using the Calculator

Examples:

• Example 1: For a solid ball with \( m = 2 \, \text{kg} \), \( r = 0.1 \, \text{m} \), axis through center, moment in kg·m²:
  • Moment: \( I = \frac{2}{5} \times 2 \times (0.1)^2 = 0.008 \, \text{kg·m²} \)
• Example 2: For a cuboid with \( m = 500 \, \text{g} \), \( l = 20 \, \text{cm} \), \( w = 10 \, \text{cm} \), \( h = 5 \, \text{cm} \), axis parallel to length, moment in kg·cm²:
  • Convert: \( m = 500 \times 0.001 = 0.5 \, \text{kg} \), \( w = 10 \times 0.01 = 0.1 \, \text{m} \), \( h = 5 \times 0.01 = 0.05 \, \text{m} \)
  • Moment: \( I = \frac{1}{12} \times 0.5 \times ((0.1)^2 + (0.05)^2) = \frac{1}{12} \times 0.5 \times 0.0125 = 0.000520833 \, \text{kg·m²} \)
  • Convert: \( 0.000520833 \times 10000 = 5.208 \, \text{kg·cm²} \)

5. Frequently Asked Questions (FAQ)

Q: What is moment of inertia?
A: Moment of inertia, also known as mass moment of inertia, is a physical property of a rotating object that quantifies its resistance to angular acceleration, depending on the distribution of its mass relative to the axis of rotation.

Q: Why does the moment of inertia depend on the axis?
A: The moment of inertia depends on how the mass is distributed relative to the axis of rotation. Mass farther from the axis contributes more to the moment of inertia, increasing resistance to rotation.

Q: What is the significance of the moment of inertia in real life?
A: It is essential in designing rotating systems (e.g., engines, wheels) and understanding rotational motion in sports, machinery, and celestial mechanics.

Moment of Inertia Calculator© - All Rights Reserved 2025