Mismatch Loss and Mismatch Uncertainty Calculator

1. What is Mismatch Loss and Mismatch Uncertainty?

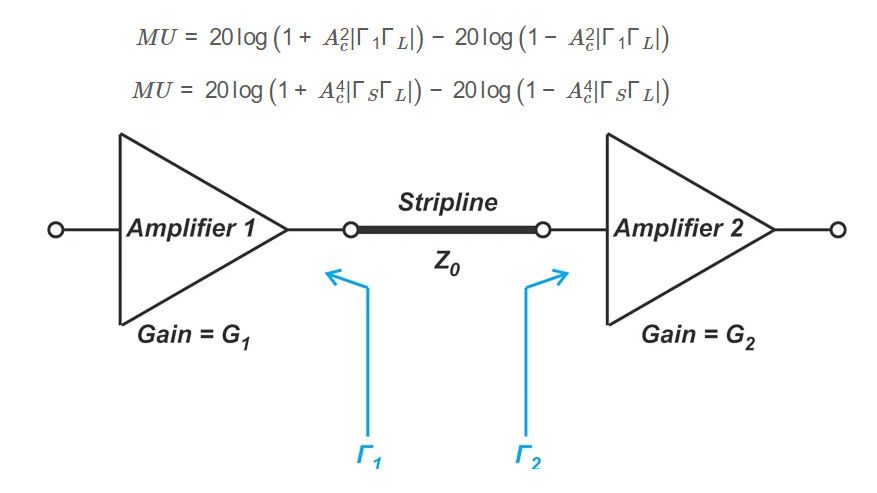
Definition: Mismatch Loss (ML) is the power loss in an RF system due to impedance mismatches causing wave reflections. Mismatch Uncertainty (MU) quantifies the range of variation in power transfer due to unknown phases of reflection coefficients.

Purpose: This calculator helps RF engineers assess the impact of impedance mismatches and the effectiveness of attenuators in reducing mismatch uncertainty, which is critical for accurate power measurements and system design.

2. How Does the Calculator Work?

The calculator uses the following formulas to compute mismatch uncertainty:

For an attenuator placed in front of a mismatched impedance: \[ MU = 20 \log \left( 1 + A_c^2 |\Gamma_1 \Gamma_L| \right) - 20 \log \left( 1 - A_c^2 |\Gamma_1 \Gamma_L| \right) \]

For an attenuator at the input port of the line: \[ MU = 20 \log \left( 1 + A_c^4 |\Gamma_S \Gamma_L| \right) - 20 \log \left( 1 - A_c^4 |\Gamma_S \Gamma_L| \right) \]

Where:

\( A_c \): Attenuation factor (\( A_c = 10^{-\text{loss_dB}/20} \))
\( |\Gamma_1| \): Magnitude of reflection coefficient at the input of the attenuator
\( |\Gamma_S| \): Magnitude of reflection coefficient at the source
\( |\Gamma_L| \): Magnitude of reflection coefficient at the load

Steps:

Enter the attenuator loss in dB.
Enter the magnitudes of the reflection coefficients \( |\Gamma_1| \), \( |\Gamma_S| \), and \( |\Gamma_L| \) (between 0 and 1).
Click "Calculate" to compute the mismatch uncertainty for both configurations.
Results are displayed in dB.

3. Importance of Mismatch Uncertainty Calculations

Mismatch uncertainty calculations are crucial for:

Accurate Measurements: Reduces errors in RF power measurements by accounting for impedance mismatches.
System Design: Helps in selecting appropriate attenuators to minimize mismatch uncertainty in RF signal chains.
Performance Optimization: Ensures maximum power transfer by mitigating the effects of reflections.

4. Using the Calculator

Examples:

Example 1: Typical Values
- Attenuator Loss: 3 dB (\( A_c = 10^{-3/20} \approx 0.707 \))
- \( |\Gamma_1| = 0.3, |\Gamma_S| = 0.3, |\Gamma_L| = 0.4 \)
- Attenuator Before Mismatched Impedance: \( MU = 20 \log \left( 1 + 0.707^2 \times 0.3 \times 0.4 \right) - 20 \log \left( 1 - 0.707^2 \times 0.3 \times 0.4 \right) \approx 0.51 \, \text{dB} \)
- Attenuator at Input Port: \( MU = 20 \log \left( 1 + 0.707^4 \times 0.3 \times 0.4 \right) - 20 \log \left( 1 - 0.707^4 \times 0.3 \times 0.4 \right) \approx 0.13 \, \text{dB} \)
Example 2: Low Reflection
- Attenuator Loss: 6 dB (\( A_c = 0.5 \))
- \( |\Gamma_1| = 0.05, |\Gamma_S| = 0.05, |\Gamma_L| = 0.05 \)
- Attenuator Before Mismatched Impedance: \( MU \approx 0.02 \, \text{dB} \)
- Attenuator at Input Port: \( MU \approx 0.00 \, \text{dB} \)
Example 3: High Attenuation
- Attenuator Loss: 10 dB (\( A_c \approx 0.316 \))
- \( |\Gamma_1| = 0.2, |\Gamma_S| = 0.2, |\Gamma_L| = 0.3 \)
- Attenuator Before Mismatched Impedance: \( MU \approx 0.11 \, \text{dB} \)
- Attenuator at Input Port: \( MU \approx 0.01 \, \text{dB} \)

5. Frequently Asked Questions (FAQ)

Q: What is mismatch uncertainty?
A: Mismatch uncertainty is the range of variation in power transfer due to unknown phases of reflection coefficients in an RF system, caused by impedance mismatches.

Q: Why use an attenuator to reduce mismatch uncertainty?
A: An attenuator reduces the magnitude of reflected waves, thereby decreasing the impact of impedance mismatches and lowering mismatch uncertainty.

Q: How does attenuator loss affect mismatch uncertainty?
A: Higher attenuator loss (lower \( A_c \)) reduces mismatch uncertainty by further attenuating reflected waves, as seen in the formulas where \( A_c^2 \) or \( A_c^4 \) scales the reflection term.

Reference

https://www.allaboutcircuits.com/technical-articles/mismatch-loss-and-mismatch-uncertainty-attenuators-and-statistical-models/