Microstrip Impedance Calculator

Dielectric Constant (\( \varepsilon_r \)):

Substrate Height (\( H \)):

Trace Width (\( W \)):

Trace Thickness (\( t \)):

1. What is a Microstrip Impedance Calculator?

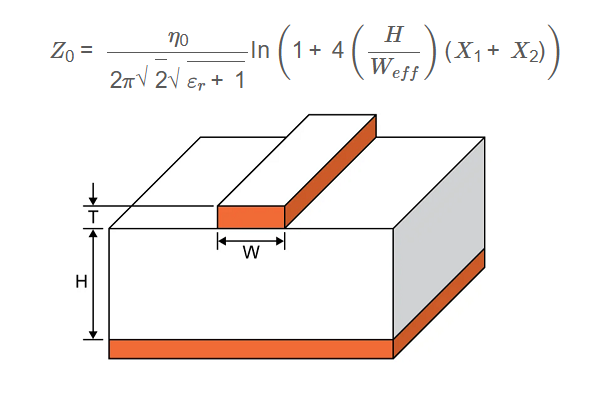
Definition: This calculator determines the characteristic impedance \( Z_0 \) of a microstrip transmission line based on the dielectric constant of the substrate (\( \varepsilon_r \)), substrate height (\( H \)), trace width (\( W \)), and trace thickness (\( t \)).

Purpose: It helps RF and PCB designers calculate the impedance of microstrip lines to ensure signal integrity, minimize reflections, and achieve proper impedance matching in high-frequency circuits.

2. How Does the Calculator Work?

The calculator uses the following formula to compute the characteristic impedance:

Characteristic Impedance \( Z_0 \): \[ Z_{0} = \frac{\eta_0}{2\pi \sqrt{2} \sqrt{\varepsilon_r + 1}} \ln \left( 1 + 4 \left( \frac{H}{W_{eff}} \right) \left( X_1 + X_2 \right) \right) \]

Where: \[ W_{eff} = W + \left( \frac{t}{\pi} \right) \ln \left\{ \frac{4e}{\sqrt{\left(\frac{t}{H}\right)^2 + \left(\frac{t}{W \pi + 1.1 t \pi}\right)^2}} \right\} \frac{\varepsilon_r + 1}{2 \varepsilon_r} \] \[ X_1 = 4 \left( \frac{14 \varepsilon_r + 8}{11 \varepsilon_r} \right) \left( \frac{H}{W_{eff}} \right) \] \[ X_2 = \sqrt{16 \left( \frac{H}{W_{eff}} \right)^2 \left( \frac{14 \varepsilon_r + 8}{11 \varepsilon_r} \right)^2 + \left( \frac{\varepsilon_r + 1}{2 \varepsilon_r} \right) \pi^2} \]

Where:

\( Z_0 \): Characteristic impedance in ohms
\( \eta_0 \approx 376.730313461 \): Free-space impedance in ohms
\( \varepsilon_r \): Dielectric constant of the substrate
\( H \): Substrate height (distance to ground plane)
\( W \): Width of the trace
\( t \): Thickness of the trace
\( W_{eff} \): Effective width of the trace, accounting for fringing fields

Unit Conversions:

Input Dimensions (\( H, W, t \)):
1 mm = 39.3701 mils
1 μm = 0.0393701 mils
Output Impedance (\( Z_0 \)):
1 ohm = 1000 mΩ

Steps:

Enter the dielectric constant \( \varepsilon_r \).
Enter the substrate height \( H \), trace width \( W \), and trace thickness \( t \), selecting the unit for each (mils, mm, or μm).
Click "Calculate" to compute \( Z_0 \).
The result is initially displayed in ohms.
Select a different unit for \( Z_0 \) (ohms or mΩ) from the dropdown after the result to convert the displayed value.

3. Importance of Microstrip Impedance Calculation

Calculating the impedance of a microstrip is crucial for:

Signal Integrity: Ensures minimal distortion in high-frequency signals.
Impedance Matching: Reduces reflections by matching the transmission line impedance to the source and load.
Design Optimization: Helps PCB designers select appropriate trace geometries for controlled impedance lines.

4. Using the Calculator

Examples:

Example 1: \( \varepsilon_r = 4.5 \), \( H = 30 \) mils, \( W = 10 \) mils, \( t = 1.4 \) mils, Result in ohms
- \( W_{eff} = 10 + \left( \frac{1.4}{\pi} \right) \ln \left\{ \frac{4e}{\sqrt{\left(\frac{1.4}{30}\right)^2 + \left(\frac{1.4}{10 \pi + 1.1 \cdot 1.4 \pi}\right)^2}} \right\} \frac{4.5 + 1}{2 \cdot 4.5} \approx 10.74 \)
- \( X_1 = 4 \left( \frac{14 \cdot 4.5 + 8}{11 \cdot 4.5} \right) \left( \frac{30}{10.74} \right) \approx 15.79 \)
- \( X_2 = \sqrt{16 \left( \frac{30}{10.74} \right)^2 \left( \frac{14 \cdot 4.5 + 8}{11 \cdot 4.5} \right)^2 + \left( \frac{4.5 + 1}{2 \cdot 4.5} \right) \pi^2} \approx 15.95 \)
- \( Z_0 = \frac{376.730313461}{2 \pi \sqrt{2} \sqrt{4.5 + 1}} \ln \left( 1 + 4 \left( \frac{30}{10.74} \right) (15.79 + 15.95) \right) \approx 105.94 \, \text{ohms} \)
Example 2: \( \varepsilon_r = 3.9 \), \( H = 0.762 \) mm, \( W = 254 \) μm, \( t = 0.0356 \) mm, Result in mΩ
- Convert: \( H = 0.762 \times 39.3701 \approx 30 \), \( W = 254 \times 0.0393701 \approx 10 \), \( t = 0.0356 \times 39.3701 \approx 1.4 \)
- \( W_{eff} \approx 10.75 \), \( X_1 \approx 15.82 \), \( X_2 \approx 15.95 \)
- \( Z_0 = \frac{376.730313461}{2 \pi \sqrt{2} \sqrt{3.9 + 1}} \ln \left( 1 + 4 \left( \frac{30}{10.75} \right) (15.82 + 15.95) \right) \approx 111.46 \, \text{ohms} \)
- Result in mΩ: \( Z_0 = 111.46 \times 1000 = 111460 \, \text{mΩ} \)
Example 3: \( \varepsilon_r = 4.2 \), \( H = 762 \) μm, \( W = 10 \) mils, \( t = 1.4 \) mils, Result in ohms
- Convert: \( H = 762 \times 0.0393701 \approx 30 \), \( W = 10 \), \( t = 1.4 \)
- \( W_{eff} \approx 10.74 \), \( X_1 \approx 15.80 \), \( X_2 \approx 15.95 \)
- \( Z_0 = \frac{376.730313461}{2 \pi \sqrt{2} \sqrt{4.2 + 1}} \ln \left( 1 + 4 \left( \frac{30}{10.74} \right) (15.80 + 15.95) \right) \approx 108.67 \, \text{ohms} \)

5. Frequently Asked Questions (FAQ)

Q: What is a microstrip transmission line?
A: A microstrip is a flat conductor on a dielectric substrate over a ground plane, widely used in RF and microwave circuits for signal transmission.

Q: Why is impedance calculation important for microstrips?
A: Accurate impedance calculation ensures proper signal integrity, minimizes reflections, and achieves impedance matching in high-frequency applications.

Q: What factors affect the accuracy of this calculation?
A: The formula assumes ideal conditions. Real-world factors like frequency-dependent dielectric constants, copper roughness, and manufacturing tolerances can affect accuracy.