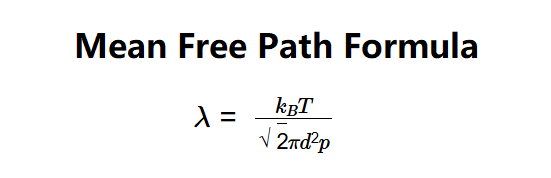Mean Free Path Calculator

Temperature (\( T \)):

Pressure (\( p \)):

Kinetic Diameter Input Method:

Select Molecule:

1. What is Mean Free Path Calculator?

Definition: This calculator computes the mean free path (\( \lambda \)), which is the average distance a gas particle travels between collisions, using the mean free path formula.

Purpose: It is used in physics and chemistry to understand gas behavior at the molecular level, particularly in applications like gas dynamics, vacuum technology, and transport phenomena.

2. How Does the Calculator Work?

The calculator uses the mean free path formula:

\( \lambda = \frac{k_B T}{\sqrt{2} \pi d^2 p} \)

Where:

\( \lambda \): Mean free path (m);
\( k_B \): Boltzmann constant (\( 1.380649 \times 10^{-23} \, \text{J/K} \));
\( T \): Temperature (K);
\( d \): Kinetic diameter of the particle (m);
\( p \): Pressure (Pa).

Steps:

Enter the temperature (\( T \)) and its unit (K, °C, or °F).
Enter the pressure (\( p \)) and its unit (Pa, kPa, bar, psi, or atm).
Choose the method to input the kinetic diameter: select a molecule from the list or enter a custom value.
If selecting a molecule, choose from the predefined list with associated kinetic diameters.
If entering a custom value, provide the kinetic diameter (\( d \)) and its unit (m, nm, or pm).
Convert all inputs to base units (K for temperature, Pa for pressure, m for diameter).
Calculate the mean free path \( \lambda \) using the formula.
Convert the result to the selected output unit (m, cm, mm, μm, or nm).
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Mean Free Path Calculation

Calculating the mean free path is crucial for:

Gas Dynamics: Understanding how gas particles move and interact, which is essential for processes like diffusion and thermal conductivity.
Vacuum Technology: Determining the behavior of gases in low-pressure environments, such as in vacuum chambers.
Material Science: Analyzing gas interactions in porous materials or thin films.

4. Using the Calculator

Example 1 (Nitrogen at Standard Conditions): Calculate the mean free path of nitrogen molecules:

Temperature: \( T = 300 \, \text{K} \);
Pressure: \( p = 101325 \, \text{Pa} \);
Molecule: Nitrogen (N₂, \( d = 3.64 \, \text{Å} = 3.64 \times 10^{-10} \, \text{m} \));
Mean Free Path: \( \lambda = \frac{(1.380649 \times 10^{-23}) \times 300}{\sqrt{2} \times \pi \times (3.64 \times 10^{-10})^2 \times 101325} \approx 6.5973 \times 10^{-8} \, \text{m} \);
Result in nm: \( \lambda = 6.5973 \times 10^{-8} \times 10^9 = 65.9730 \, \text{nm} \).

Example 2 (Custom Diameter): Calculate the mean free path with a custom diameter:

Temperature: \( T = 25 \, \text{°C} \);
Pressure: \( p = 1 \, \text{atm} \);
Custom Diameter: \( d = 370 \, \text{pm} \);
Convert units: \( T = 25 + 273.15 = 298.15 \, \text{K} \), \( p = 1 \times 101325 = 101325 \, \text{Pa} \), \( d = 370 \times 10^{-12} = 3.7 \times 10^{-10} \, \text{m} \);
Mean Free Path: \( \lambda \approx 6.7345 \times 10^{-8} \, \text{m} \);
Result in μm: \( \lambda = 6.7345 \times 10^{-8} \times 10^6 \approx 0.0673 \, \text{μm} \).

5. Frequently Asked Questions (FAQ)

Q: What is the mean free path?
A: The mean free path is the average distance a gas particle travels between successive collisions with other particles.

Q: How does temperature affect the mean free path?
A: The mean free path is directly proportional to temperature; as temperature increases, the mean free path increases because particles move faster and are less densely packed.

Q: Why is the kinetic diameter important?
A: The kinetic diameter represents the effective size of the gas particle, which affects the collision frequency; a larger diameter leads to more frequent collisions and a shorter mean free path.