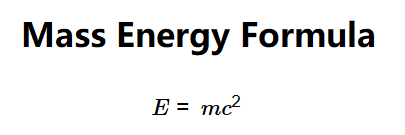Mass-Energy Equivalence Calculator

1. What is Mass-Energy Equivalence Calculator?

Definition: This calculator computes the rest energy (\( E \)) of an object based on its mass (\( m \)), using Einstein's famous mass-energy equivalence formula.

Purpose: It is used in physics to understand the energy equivalent of a given mass, illustrating the profound relationship between mass and energy as described by special relativity.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula:

\( E = m c^2 \)

Where:

\( E \): Rest energy (J, kJ, MJ, GJ, eV, keV, MeV)
\( m \): Mass of the object (kg, g, mg, lb, oz)
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \))

Unit Conversions:

Mass (\( m \)):
- 1 kg = 1 kg
- 1 g = \( 10^{-3} \) kg
- 1 mg = \( 10^{-6} \) kg
- 1 lb = 0.453592 kg
- 1 oz = 0.0283495 kg
Energy (\( E \)):
- 1 J = 1 J
- 1 kJ = \( 10^3 \) J
- 1 MJ = \( 10^6 \) J
- 1 GJ = \( 10^9 \) J
- 1 eV = \( 1.602 \times 10^{-19} \) J
- 1 keV = \( 1.602 \times 10^{-16} \) J
- 1 MeV = \( 1.602 \times 10^{-13} \) J

Steps:

Enter the mass (\( m \)) with its respective unit (kg, g, mg, lb, oz).
Convert the mass to kilograms.
Calculate the rest energy using \( E = m c^2 \).
Select the desired unit for the energy result (J, kJ, MJ, GJ, eV, keV, MeV).
Convert the energy to the selected unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Mass-Energy Equivalence Calculation

Calculating mass-energy equivalence is crucial for:

Understanding Special Relativity: The formula \( E = m c^2 \) is a cornerstone of Einstein's theory of special relativity, showing that mass and energy are interchangeable.
Nuclear Physics: It explains the energy released in nuclear reactions, such as fission and fusion, where small amounts of mass are converted into large amounts of energy.
Energy Applications: It provides insight into the potential energy stored in matter, relevant for technologies like nuclear power and particle physics experiments.

4. Using the Calculator

Examples:

Example 1: Calculate the rest energy of an object with a mass of 1 kg, with the result in joules:
- Enter \( m = 1 \) kg.
- \( E = 1 \times (299,792,458)^2 \approx 8.99 \times 10^{16} \) J
- Result: \( E = 8.9900e16 \) J
Example 2: Calculate the rest energy of an object with a mass of 1 g, with the result in MeV:
- Enter \( m = 1 \) g.
- Convert to kg: \( m = 1 \times 10^{-3} = 0.001 \) kg.
- \( E = 0.001 \times (299,792,458)^2 \approx 8.99 \times 10^{13} \) J
- Convert to MeV: \( E = 8.99 \times 10^{13} / (1.602 \times 10^{-13}) \approx 5.611 \times 10^{26} \) MeV
- Result: \( E = 5.6110e26 \) MeV

5. Frequently Asked Questions (FAQ)

Q: What does \( E = m c^2 \) mean?
A: The equation \( E = m c^2 \) means that the energy (\( E \)) of an object at rest is equal to its mass (\( m \)) multiplied by the speed of light (\( c \)) squared, showing that mass can be converted into energy.

Q: Why is the speed of light squared in the formula?
A: The speed of light (\( c \)) is squared because it represents the conversion factor between mass and energy in the framework of special relativity. Since \( c \) is a very large number (\( 299,792,458 \, \text{m/s} \)), squaring it results in a large factor, meaning even a small mass can produce a significant amount of energy.

Q: Can this calculator be used for objects moving at high speeds?
A: This calculator computes the rest energy, which applies to objects at rest. For moving objects, the total energy would include kinetic energy, requiring a more complex relativistic formula.