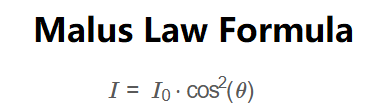Malus's Law Calculator

1. What is Malus's Law Calculator?

Definition: This calculator computes the output intensity (\( I \)) of polarized light passing through a polarizer using Malus's Law, which relates the intensity to the angle between the light's polarization and the polarizer's axis.

Purpose: It is used in optics to analyze the behavior of polarized light, such as in photography, optical experiments, and the design of polarizing filters.

2. How Does the Calculator Work?

The calculator uses Malus's Law:

Formula: \[ I = I_0 \cdot \cos^2(\theta) \] Where:

\( I \): Output intensity (W/m², mW/m², μW/m², nW/m²)
\( I_0 \): Initial intensity of the incident light (W/m², mW/m², μW/m², nW/m²)
\( \theta \): Angle between the light's polarization and the polarizer's axis (degrees or radians)

Unit Conversions:

Intensity (\( I \), \( I_0 \)): W/m², mW/m² (1 mW/m² = \( 10^{-3} \) W/m²), μW/m² (1 μW/m² = \( 10^{-6} \) W/m²), nW/m² (1 nW/m² = \( 10^{-9} \) W/m²)
Angle (\( \theta \)): degrees (1 degree = \( \pi/180 \) radians), radians

Steps:

Enter the initial intensity (\( I_0 \)) and angle (\( \theta \)), and select their units.
Convert intensity to W/m² and angle to radians if necessary.
Calculate the output intensity using Malus's Law: \( I = I_0 \cdot \cos^2(\theta) \).
Convert the result to the selected intensity unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Malus's Law Calculation

Calculating the output intensity using Malus's Law is crucial for:

Optical Experiments: Understanding the behavior of polarized light in physics experiments.
Photography: Using polarizing filters to reduce glare and control light intensity.
Display Technology: Designing LCD screens that rely on polarization to control light transmission.

4. Using the Calculator

Examples:

Example 1: For \( I_0 = 100 \, \text{W/m²} \), \( \theta = 30 \, \text{degrees} \), output intensity in W/m²:
- Convert: \( \theta = 30 \times \pi/180 = \pi/6 \, \text{radians} \)
- Calculate: \( I = 100 \cdot \cos^2(\pi/6) = 100 \cdot (0.866)^2 \approx 75 \, \text{W/m²} \)
Example 2: For \( I_0 = 50 \, \text{mW/m²} \), \( \theta = 1.5708 \, \text{radians} \), output intensity in mW/m²:
- Convert: \( I_0 = 50 \times 10^{-3} = 0.05 \, \text{W/m²} \), \( \theta = 1.5708 \, \text{radians} \approx \pi/2 \)
- Calculate: \( I = 0.05 \cdot \cos^2(\pi/2) = 0.05 \cdot 0 = 0 \, \text{W/m²} \), in mW/m²: \( 0 \times 10^3 = 0 \, \text{mW/m²} \)

5. Frequently Asked Questions (FAQ)

Q: What is Malus's Law?
A: Malus's Law describes how the intensity of polarized light changes when passing through a polarizer, based on the angle between the light's polarization and the polarizer's axis.

Q: Why does the intensity decrease with the angle?
A: The intensity decreases because the component of the light's electric field aligned with the polarizer's axis is proportional to \( \cos(\theta) \), and intensity depends on the square of the field amplitude, hence \( \cos^2(\theta) \).

Q: What happens when the angle is 90 degrees?
A: When \( \theta = 90^\circ \), \( \cos(90^\circ) = 0 \), so the output intensity is zero, meaning no light passes through the polarizer.