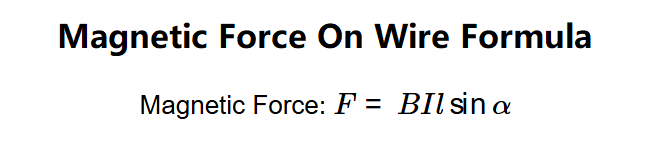Magnetic Force on Current-Carrying Wire Calculator

Magnetic Force on Current-Carrying Wire Formula

Magnetic Field Strength (\( B \)):

Current (\( I \)):

Length of the Wire (\( l \)):

Angle (\( \alpha \)) (degrees):

1. What is Magnetic Force on Current-Carrying Wire Calculator?

Definition: This calculator computes the magnetic force (\( F \)) acting on a straight current-carrying wire placed in a magnetic field, taking into account the angle (\( \alpha \)) between the current and the magnetic field.

Purpose: It is used in physics and electrical engineering to analyze the forces on current-carrying conductors in magnetic fields, which is important for understanding the operation of motors, generators, and other electromagnetic devices.

2. How Does the Calculator Work?

The calculator uses the following formula:

Magnetic Force: \( F = B I l \sin \alpha \)

Where:

\( B \): Magnetic field strength (T)
\( I \): Current in the wire (A)
\( l \): Length of the wire (m)
\( \alpha \): Angle between the current and magnetic field (degrees)
\( F \): Magnetic force (N)

Steps:

Enter the magnetic field strength (\( B \)), current (\( I \)), length of the wire (\( l \)), and angle (\( \alpha \)) with their units. The angle defaults to 90 degrees if not specified.
Convert all inputs to base units (T, A, m).
Calculate the magnetic force using the formula, with \( \alpha \) converted to radians for the \( \sin \) function.
Convert the result to the selected output unit (N, mN, µN).
Display the result: if the value is less than 0.001 in the selected unit, use scientific notation; otherwise, display with 4 decimal places.

3. Importance of Magnetic Force on Current-Carrying Wire Calculation

Calculating the magnetic force on a current-carrying wire is crucial for:

Electromagnetic Devices: Understanding the forces in motors, generators, and solenoids, where current-carrying wires interact with magnetic fields to produce motion or energy.
Design and Safety: Ensuring that the forces on wires in high-current applications do not cause mechanical failure or unwanted movement.
Educational Purposes: Demonstrating fundamental principles of electromagnetism, such as the Lorentz force, with the ability to explore the effect of the angle \( \alpha \).

4. Using the Calculator

Example 1 (Angle = 90°): Calculate the magnetic force on a wire with \( B = 0.5 \, \text{T} \), \( I = 2 \, \text{A} \), \( l = 1 \, \text{m} \), and \( \alpha = 90^\circ \):

Magnetic Field Strength (\( B \)): 0.5 T
Current (\( I \)): 2 A
Length of the Wire (\( l \)): 1 m
Angle (\( \alpha \)): 90°
Magnetic Force (\( F \)): \( 0.5 \times 2 \times 1 \times \sin(90^\circ) = 0.5 \times 2 \times 1 \times 1 = 1 \, \text{N} \)
Result: \( F = 1.0000 \, \text{N} \)

Example 2 (Angle = 30° with Scientific Notation): Calculate the magnetic force on a wire with \( B = 10 \, \text{mT} \), \( I = 1 \, \text{mA} \), \( l = 10 \, \text{cm} \), and \( \alpha = 30^\circ \):

Magnetic Field Strength (\( B \)): 10 mT = \( 0.01 \, \text{T} \)
Current (\( I \)): 1 mA = \( 0.001 \, \text{A} \)
Length of the Wire (\( l \)): 10 cm = \( 0.1 \, \text{m} \)
Angle (\( \alpha \)): 30°
Magnetic Force (\( F \)): \( 0.01 \times 0.001 \times 0.1 \times \sin(30^\circ) = 0.01 \times 0.001 \times 0.1 \times 0.5 = 0.0000005 \, \text{N} \), in µN: \( 0.0000005 \times 10^6 = 0.5 \, \text{µN} \)
Result: \( F = 0.5000 \, \text{µN} \)

5. Frequently Asked Questions (FAQ)

Q: What is the magnetic force on a current-carrying wire?
A: The magnetic force on a current-carrying wire is the force exerted on the wire due to the interaction between the current and an external magnetic field. It depends on the angle (\( \alpha \)) between the current and the magnetic field.

Q: Why does the angle matter?
A: The angle (\( \alpha \)) determines the component of the magnetic field perpendicular to the current, which produces the force. The force is maximum when \( \alpha = 90^\circ \) (\( \sin \alpha = 1 \)) and zero when \( \alpha = 0^\circ \) or \( 180^\circ \) (\( \sin \alpha = 0 \)).

Q: What happens if the current and magnetic field are parallel?
A: If the current and magnetic field are parallel (\( \alpha = 0^\circ \)), the force is zero because \( \sin 0 = 0 \). Similarly, if they are antiparallel (\( \alpha = 180^\circ \)), the force is also zero.