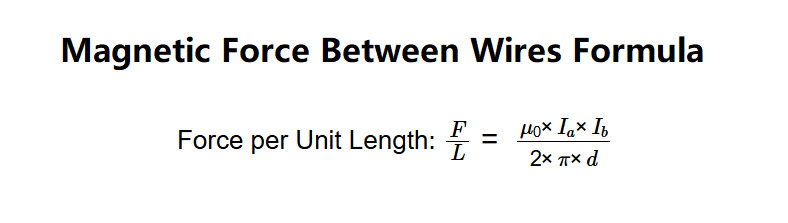Magnetic Force Between Wires Calculator

Current in First Wire (\( I_a \)):

Current in Second Wire (\( I_b \)):

Distance Between Wires (\( d \)):

1. What is Magnetic Force Between Wires Calculator?

Definition: This calculator computes the magnetic force per unit length (\( \frac{F}{L} \)) acting on each wire due to the magnetic interaction between two parallel, straight, current-carrying wires.

Purpose: It is used in physics and electrical engineering to analyze the magnetic forces between current-carrying conductors, which is important for understanding electromagnetic interactions in circuits, motors, and other devices.

2. How Does the Calculator Work?

The calculator uses the following formula:

Force per Unit Length: \( \frac{F}{L} = \frac{\mu_0 \times I_a \times I_b}{2 \times \pi \times d} \)

Where:

\( \mu_0 \): Permeability of free space (\( 4 \times \pi \times 10^{-7} \, \text{T} \cdot \text{m} / \text{A} \))
\( I_a \): Current in the first wire (A)
\( I_b \): Current in the second wire (A)
\( d \): Distance between the wires (m)
\( \frac{F}{L} \): Force per unit length (N/m)

Steps:

Enter the currents in the first and second wires (\( I_a \), \( I_b \)) and the distance between the wires (\( d \)) with their units.
Convert all inputs to base units (A, m).
Calculate the force per unit length using the formula.
Convert the result to the selected output unit (N/m, mN/m, µN/m).
Display the result: if the value is less than 0.001 in the selected unit, use scientific notation; otherwise, display with 4 decimal places.

3. Importance of Magnetic Force Between Wires Calculation

Calculating the magnetic force between wires is crucial for:

Electromagnetic Design: Understanding the forces between current-carrying conductors in motors, transformers, and other electromagnetic devices.
Wire Stability: Ensuring that the forces between wires do not cause mechanical issues, such as unwanted movement or deformation in high-current applications.
Educational Purposes: Demonstrating fundamental principles of electromagnetism, such as the Biot-Savart Law and Ampère's force law, in a simplified form.

4. Using the Calculator

Example 1: Calculate the force per unit length between two wires with \( I_a = 5 \, \text{A} \), \( I_b = 3 \, \text{A} \), and \( d = 2 \, \text{cm} \):

Current in First Wire (\( I_a \)): 5 A
Current in Second Wire (\( I_b \)): 3 A
Distance Between Wires (\( d \)): 2 cm = \( 0.02 \, \text{m} \)
Force per Unit Length (\( \frac{F}{L} \)): \( \frac{(4 \times \pi \times 10^{-7}) \times 5 \times 3}{2 \times \pi \times 0.02} = \frac{4 \times 10^{-7} \times 15}{0.04} = 1.5 \times 10^{-4} \, \text{N/m} \), in µN/m: \( 1.5 \times 10^{-4} \times 10^6 = 150 \, \text{µN/m} \)
Result: \( \frac{F}{L} = 150.0000 \, \text{µN/m} \)

Example 2 (Demonstrating Scientific Notation): Calculate the force per unit length between two wires with \( I_a = 10 \, \text{mA} \), \( I_b = 20 \, \text{mA} \), and \( d = 1 \, \text{mm} \):

Current in First Wire (\( I_a \)): 10 mA = \( 0.01 \, \text{A} \)
Current in Second Wire (\( I_b \)): 20 mA = \( 0.02 \, \text{A} \)
Distance Between Wires (\( d \)): 1 mm = \( 0.001 \, \text{m} \)
Force per Unit Length (\( \frac{F}{L} \)): \( \frac{(4 \times \pi \times 10^{-7}) \times 0.01 \times 0.02}{2 \times \pi \times 0.001} = \frac{4 \times 10^{-7} \times 0.0002}{0.002} = 4 \times 10^{-8} \, \text{N/m} \), in µN/m: \( 4 \times 10^{-8} \times 10^6 = 0.04 \, \text{µN/m} \)
Result: \( \frac{F}{L} = 0.0400 \, \text{µN/m} \)

5. Frequently Asked Questions (FAQ)

Q: What is the magnetic force between wires?
A: The magnetic force between wires is the force exerted on each wire due to the magnetic fields generated by the currents flowing in them. If the currents flow in the same direction, the wires attract each other; if in opposite directions, they repel.

Q: Why is the force per unit length used?
A: The force per unit length (\( \frac{F}{L} \)) is used because the force depends on the length of the wires. For infinitely long wires, this value is constant, and the total force on a wire of length \( L \) is \( F = \frac{F}{L} \times L \).

Q: What does a positive or negative force per unit length mean?
A: The calculator provides the magnitude of the force per unit length. A positive value indicates the force's magnitude, but the direction (attractive or repulsive) depends on the current directions, which are not specified in the input.