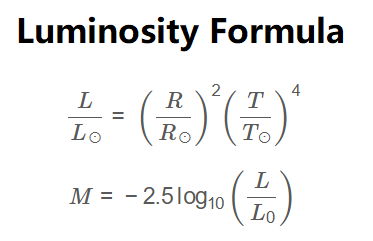Luminosity Calculator

Radius of the Star (\( R \)):

Temperature of the Star (\( T \)):

Distance to the Star (\( d \)):

Luminosity (\( L \)):

Absolute Magnitude (\( M \)):

Apparent Magnitude (\( m \)):

1. What is Luminosity Calculator?

Definition: This calculator computes the luminosity (\( L \)), absolute magnitude (\( M \)), and apparent magnitude (\( m \)) of a star, based on the star's radius (\( R \)), temperature (\( T \)), and distance (\( d \)).

Purpose: It is used in astronomy to estimate a star's energy output and brightness as seen from Earth, helping to classify stars and understand their properties compared to the Sun.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ \frac{L}{L_\odot} = \left(\frac{R}{R_\odot}\right)^2 \left(\frac{T}{T_\odot}\right)^4 \] \[ M = -2.5 \log_{10} \left(\frac{L}{L_0}\right) \] \[ m = M + 5 \log_{10} \left(\frac{d}{10}\right) \] Where:

\( L \): Luminosity of the star (W, GW, TW, PW, solar luminosities)
\( L_\odot \): Luminosity of the Sun (\( 3.828 \times 10^{26} \, \text{W} \))
\( R \): Radius of the star (m, km, mi, solar radii)
\( R_\odot \): Radius of the Sun (\( 695,700 \, \text{km} \))
\( T \): Temperature of the star (K, °C, °F)
\( T_\odot \): Temperature of the Sun (\( 5778 \, \text{K} \))
\( d \): Distance to the star (m, km, mi, ly, au, pc)
\( M \): Absolute magnitude of the star (dimensionless)
\( m \): Apparent magnitude of the star (dimensionless)
\( L_0 \): Zero-point luminosity (\( 3.0128 \times 10^{28} \, \text{W} \))

Unit Conversions:

Radius (\( R \)):
- 1 m = 0.001 km
- 1 km = 1 km
- 1 mi = 1.60934 km
- 1 solar radius = \( 695,700 \, \text{km} \)
Temperature (\( T \)):
- 1 K = 1 K
- 1 °C = K - 273.15
- 1 °F = (K - 273.15) × 9/5 + 32
Distance (\( d \)):
- 1 m = \( \frac{1}{3.08568 \times 10^{16}} \) pc
- 1 km = \( \frac{1}{3.08568 \times 10^{13}} \) pc
- 1 mi = \( \frac{1}{1.91741 \times 10^{12}} \) pc
- 1 ly = \( \frac{1}{3.262} \) pc
- 1 au = \( \frac{1}{206,265} \) pc
- 1 pc = 1 pc
Luminosity (\( L \)):
- 1 W = 1 W
- 1 GW = \( 10^9 \) W
- 1 TW = \( 10^{12} \) W
- 1 PW = \( 10^{15} \) W
- 1 solar luminosity = \( 3.828 \times 10^{26} \) W
Absolute Magnitude (\( M \)): Dimensionless, no conversion needed.
Apparent Magnitude (\( m \)): Dimensionless, no conversion needed.

Steps:

Enter the radius of the star (\( R \)) with its respective unit (m, km, mi, solar radii).
Enter the temperature of the star (\( T \)) with its respective unit (K, °C, °F).
Enter the distance to the star (\( d \)) with its respective unit (m, km, mi, ly, au, pc).
Select the desired unit for the luminosity result (W, GW, TW, PW, solar luminosities).
Convert the radius to kilometers.
Convert the temperature to Kelvin.
Convert the distance to parsecs.
Calculate the luminosity ratio using \( \frac{L}{L_\odot} = \left(\frac{R}{R_\odot}\right)^2 \left(\frac{T}{T_\odot}\right)^4 \).
Calculate the luminosity \( L \) in watts by multiplying the ratio by \( L_\odot \).
Convert the luminosity to the selected unit.
Calculate the absolute magnitude using \( M = -2.5 \log_{10} \left(\frac{L}{L_0}\right) \).
Calculate the apparent magnitude using \( m = M + 5 \log_{10} \left(\frac{d}{10}\right) \).
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Luminosity Calculation

Calculating a star's luminosity, absolute magnitude, and apparent magnitude is crucial for:

Stellar Classification: Determining a star's energy output and brightness helps classify it on the Hertzsprung-Russell diagram.
Distance Measurement: Apparent magnitude, combined with absolute magnitude, allows astronomers to estimate distances to stars.
Astrophysical Models: Understanding a star's properties aids in modeling its evolution and lifecycle.

4. Using the Calculator

Examples:

Example 1: Calculate the luminosity, absolute magnitude, and apparent magnitude of the Sun (\( R = 695,700 \, \text{km} \), \( T = 5778 \, \text{K} \), \( d = 4.848 \times 10^{-6} \, \text{pc} \), approximately 1 AU), with luminosity in solar luminosities:
- Enter \( R = 695,700 \) km.
- Enter \( T = 5778 \) K.
- Enter \( d = 4.848 \times 10^{-6} \) pc (1 AU = \( \frac{1}{206,265} \) pc).
- \( \frac{L}{L_\odot} = \left(\frac{695,700}{695,700}\right)^2 \left(\frac{5778}{5778}\right)^4 = 1 \)
- \( L = 1 \times 3.828 \times 10^{26} \) W
- Convert to solar luminosities: \( L = 1 \) \( L_\odot \)
- \( M = -2.5 \log_{10} \left(\frac{3.828 \times 10^{26}}{3.0128 \times 10^{28}}\right) \approx 4.7400 \)
- \( m = 4.7400 + 5 \log_{10} \left(\frac{4.848 \times 10^{-6}}{10}\right) \approx 4.7400 - 31.8195 \approx -27.0795 \)
- Result: \( L = 1.0000 \) \( L_\odot \), \( M = 4.7400 \), \( m = -27.0795 \)
Example 2: Calculate the luminosity, absolute magnitude, and apparent magnitude of a star with \( R = 2 \, R_\odot \), \( T = 37.04 \, \text{°C} \), \( d = 10 \, \text{pc} \), with luminosity in gigawatts:
- Enter \( R = 2 \) solar radii.
- Convert to km: \( R = 2 \times 695,700 = 1,391,400 \, \text{km} \)
- Enter \( T = 37.04 \) °C.
- Convert to K: \( T = 37.04 + 273.15 = 310.19 \, \text{K} \)
- Enter \( d = 10 \) pc.
- \( \frac{L}{L_\odot} = \left(\frac{1,391,400}{695,700}\right)^2 \left(\frac{310.19}{5778}\right)^4 \approx 4 \times 8.312 \times 10^{-6} \approx 3.3248 \times 10^{-5} \)
- \( L = 3.3248 \times 10^{-5} \times 3.828 \times 10^{26} \approx 1.2728e22 \) W
- Convert to gigawatts: \( L = 1.2728e22 / 10^9 \approx 1.2728e13 \) GW
- \( M = -2.5 \log_{10} \left(\frac{1.2728e22}{3.0128e28}\right) \approx 16.4325 \)
- \( m = 16.4325 + 5 \log_{10} \left(\frac{10}{10}\right) = 16.4325 + 0 = 16.4325 \)
- Result: \( L = 1.2728e13 \) GW, \( M = 16.4325 \), \( m = 16.4325 \)

5. Frequently Asked Questions (FAQ)

Q: What is the difference between absolute and apparent magnitude?
A: Absolute magnitude (\( M \)) is a star's brightness if it were 10 parsecs away, while apparent magnitude (\( m \)) is how bright it appears from Earth, affected by its distance.

Q: Why does temperature need to be in Kelvin?
A: The luminosity formula uses the Stefan-Boltzmann law, which requires temperature in Kelvin to ensure accurate calculations based on physical laws.

Q: How is apparent magnitude useful?
A: Apparent magnitude helps astronomers determine how bright a star appears in the sky, which is essential for observing and comparing stars from Earth.