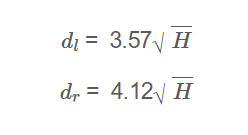Line of Sight Calculator (Single Antenna)

1. What is Line of Sight Calculator (Single Antenna)?

Definition: This calculator determines the line-of-sight distance and radio horizon service range for a single antenna, accounting for the Earth's curvature and atmospheric refraction.

Purpose: It is used in RF engineering to estimate the maximum distance a signal can travel from an antenna, useful for planning wireless communication links.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ d_l = 3.57 \sqrt{H} \] \[ d_r = 4.12 \sqrt{H} \] Where:

\( d_l \): Line of Sight Distance (km, mi, m, ft)
\( d_r \): Radio Horizon - Service Range (km, mi, m, ft)
\( H \): Antenna Height (m)

Unit Conversions:

Antenna Height:
- 1 m = 1 meter
- 1 km = 1,000 m
- 1 ft = 0.3048 m
- 1 mi = 1,609.344 m
Distances:
- 1 km = 1 kilometer
- 1 mi = 0.621371 km
- 1 m = 0.001 km
- 1 ft = 0.0003048 km

Steps:

Enter the Antenna Height (non-negative value) and select the unit (m, km, ft, mi).
Convert height to meters.
Calculate \( d_l \) and \( d_r \) in kilometers using the formulas.
Convert the results to the selected unit (km, mi, m, ft).
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Line of Sight Calculation

Calculating the Line of Sight Distance and Service Range is crucial for:

Wireless Communication: Estimating the range of microwave, radio, or satellite links.
Network Planning: Determining the coverage area of a single antenna in telecom systems.
RF Engineering: Optimizing antenna placement for maximum coverage without obstructions.

4. Using the Calculator

Examples:

Example 1: For \( H = 30 \, \text{m} \), results in kilometers:
- \( d_l = 3.57 \sqrt{30} \approx 3.57 \times 5.4772 \approx 19.5536 \, \text{km} \)
- \( d_r = 4.12 \sqrt{30} \approx 4.12 \times 5.4772 \approx 22.5661 \, \text{km} \)
Example 2: For \( H = 100 \, \text{ft} \), results in miles:
- Convert to meters: \( H = 100 \times 0.3048 = 30.48 \, \text{m} \)
- \( d_l = 3.57 \sqrt{30.48} \approx 3.57 \times 5.5207 \approx 19.7090 \, \text{km} \)
- \( d_r = 4.12 \sqrt{30.48} \approx 4.12 \times 5.5207 \approx 22.7453 \, \text{km} \)
- Convert to miles: \( d_l \approx 12.2478 \, \text{mi} \), \( d_r \approx 14.1335 \, \text{mi} \)

5. Frequently Asked Questions (FAQ)

Q: What is the difference between line of sight distance and service range?
A: Line of sight distance (\( d_l \)) uses a standard refraction model (3.57 constant) for direct visibility, while service range (\( d_r \)) uses a different constant (4.12) for radio horizons, often considering additional factors like signal propagation.

Q: Why does the Earth's curvature matter?
A: The Earth's curvature limits the maximum distance for line-of-sight communication, as the signal path bends over long distances.

Q: How does antenna height affect the distance?
A: Higher antennas increase both the line-of-sight distance and service range by allowing the signal to clear the Earth's curvature over a longer range.