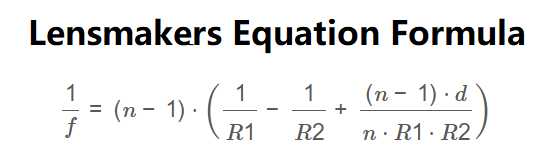Lensmaker's Equation Calculator

Refractive Index (\( n \)):

Radius of Curvature (\( R1 \)) (closest to light source):

Radius of Curvature (\( R2 \)) (farthest from light source):

Lens Thickness (\( d \)):

1. What is Lensmaker's Equation Calculator?

Definition: This calculator computes the focal length (\( f \)) of a lens in air using the lensmaker's equation, which relates the lens's geometry and material properties to its focusing power.

Purpose: It is used in optics to design lenses for various applications, such as cameras, microscopes, and laser systems, by determining the focal length based on the lens's shape and material.

2. How Does the Calculator Work?

The calculator uses the lensmaker's equation:

Formula: \[ \frac{1}{f} = (n - 1) \cdot \left( \frac{1}{R1} - \frac{1}{R2} + \frac{(n - 1) \cdot d}{n \cdot R1 \cdot R2} \right) \] Where:

\( f \): Focal length of the lens (nm, μm, mm, cm, m, in, ft, yd)
\( n \): Refractive index of the lens material (dimensionless)
\( R1 \): Radius of curvature of the lens surface closest to the light source (nm, μm, mm, cm, m, in, ft, yd)
\( R2 \): Radius of curvature of the lens surface farthest from the light source (nm, μm, mm, cm, m, in, ft, yd)
\( d \): Thickness of the lens (nm, μm, mm, cm, m, in, ft, yd)

Unit Conversions:

Radius of Curvature (\( R1 \), \( R2 \)), Thickness (\( d \)), Focal Length (\( f \)): nm (1 nm = \( 10^{-9} \) m), μm (1 μm = \( 10^{-6} \) m), mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)

Steps:

Enter the refractive index (\( n \)), radii of curvature (\( R1 \), \( R2 \)), and lens thickness (\( d \)), and select their units.
Convert all length inputs to meters.
Calculate \( \frac{1}{f} \) using the lensmaker's equation.
Compute the focal length \( f = \frac{1}{\frac{1}{f}} \).
Convert the result to the selected unit (nm, μm, mm, cm, m, in, ft, yd).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Focal Length Calculation

Calculating the focal length of a lens is crucial for:

Optical Design: Designing lenses for cameras, telescopes, microscopes, and laser systems by determining their focusing properties.
Vision Correction: Creating corrective lenses for eyeglasses and contact lenses based on the required focal length.
Education: Understanding the relationship between lens geometry, material, and optical performance in physics and optics.

4. Using the Calculator

Examples:

Example 1: For \( n = 1.5 \), \( R1 = 20 \, \text{cm} \), \( R2 = -20 \, \text{cm} \), \( d = 2 \, \text{mm} \), focal length in cm:
- Convert: \( R1 = 20 \times 0.01 = 0.2 \, \text{m} \), \( R2 = -20 \times 0.01 = -0.2 \, \text{m} \), \( d = 2 \times 0.001 = 0.002 \, \text{m} \)
- Calculate: \( \frac{1}{f} = (1.5 - 1) \cdot \left( \frac{1}{0.2} - \frac{1}{-0.2} + \frac{(1.5 - 1) \times 0.002}{1.5 \times 0.2 \times (-0.2)} \right) \approx 0.05 \)
- Focal Length: \( f = \frac{1}{0.05} = 20 \, \text{m} \), in cm: \( 20 \times 100 = 2000 \, \text{cm} \)
Example 2: For \( n = 1.6 \), \( R1 = 50 \, \text{mm} \), \( R2 = \infty \) (flat surface), \( d = 5 \, \text{mm} \), focal length in mm:
- Convert: \( R1 = 50 \times 0.001 = 0.05 \, \text{m} \), \( R2 = \infty \), \( d = 5 \times 0.001 = 0.005 \, \text{m} \)
- Calculate: \( \frac{1}{f} = (1.6 - 1) \cdot \left( \frac{1}{0.05} - \frac{1}{\infty} + \frac{(1.6 - 1) \times 0.005}{1.6 \times 0.05 \times \infty} \right) \approx 0.012 \)
- Focal Length: \( f = \frac{1}{0.012} \approx 83.3333 \, \text{m} \), in mm: \( 83.3333 \times 1000 \approx 83333.3333 \, \text{mm} \)

5. Frequently Asked Questions (FAQ)

Q: What is the lensmaker's equation?
A: The lensmaker's equation relates the focal length of a lens to its refractive index, radii of curvature, and thickness, allowing the calculation of the lens's focusing power in air.

Q: What does a negative radius of curvature mean?
A: A negative radius of curvature (e.g., for \( R1 \) or \( R2 \)) indicates that the lens surface is concave relative to the light source, while a positive radius indicates a convex surface.

Q: Why must the refractive index be greater than 1?
A: The refractive index (\( n \)) must be greater than 1 because the lens material must have a higher refractive index than air (which has \( n = 1 \)) to bend light and focus it.