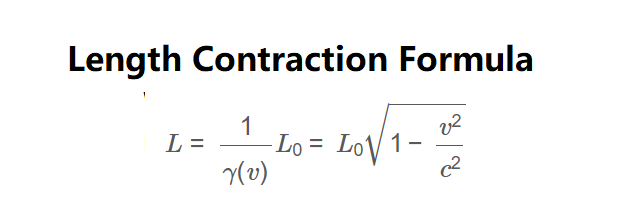Length Contraction Calculator

Proper Length (\( L_0 \)):

Speed (\( v \)):

1. What is Length Contraction Calculator?

Definition: This calculator computes the observed length (\( L \)) of an object in motion, based on its proper length (\( L_0 \)) and speed (\( v \)), using the principles of special relativity.

Purpose: It is used in physics to understand how lengths contract when objects move at relativistic speeds, a phenomenon predicted by Einstein's theory of special relativity.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula:

\( L = \frac{1}{\gamma(v)} L_0 = L_0 \sqrt{1 - \frac{v^2}{c^2}} \)

Where:

\( L \): Observed length (m, km, mi, cm, mm, in, ft, yd)
\( L_0 \): Proper length (m, km, mi, cm, mm, in, ft, yd)
\( v \): Speed of the object (m/s, km/h, mph, fraction of c)
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \))
\( \gamma(v) \): Lorentz factor, defined as \( \gamma(v) = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \)

Unit Conversions:

Length (\( L_0 \), \( L \)):
- 1 m = 1 m
- 1 km = 1000 m
- 1 mi = 1609.344 m
- 1 cm = 0.01 m
- 1 mm = 0.001 m
- 1 in = 0.0254 m
- 1 ft = 0.3048 m
- 1 yd = 0.9144 m
Speed (\( v \)):
- 1 m/s = 1 m/s
- 1 km/h = \( \frac{1000}{3600} \) m/s
- 1 mph = \( \frac{1609.344}{3600} \) m/s
- 1 c = \( 299,792,458 \) m/s

Steps:

Enter the proper length (\( L_0 \)) with its respective unit (m, km, mi, cm, mm, in, ft, yd).
Enter the speed (\( v \)) with its respective unit (m/s, km/h, mph, fraction of c).
Convert the proper length to meters.
Convert the speed to meters per second.
Calculate the Lorentz factor \( \gamma(v) = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \).
Calculate the observed length \( L = \frac{L_0}{\gamma(v)} \).
Select the desired unit for the observed length (m, km, mi, cm, mm, in, ft, yd).
Convert the observed length to the selected unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Length Contraction Calculation

Calculating length contraction is crucial for:

Understanding Special Relativity: Length contraction is a fundamental effect of Einstein's theory of special relativity, showing how space and time are interconnected.
High-Speed Physics: It is essential for experiments involving particles moving at relativistic speeds, such as in particle accelerators.
Space Travel Concepts: Length contraction affects theoretical models of high-speed space travel, impacting perceived distances.

4. Using the Calculator

Examples:

Example 1: Calculate the observed length of a spaceship with a proper length of 100 meters traveling at 0.6c:
- Enter \( L_0 = 100 \) m.
- Enter \( v = 0.6 \) c.
- Convert speed: \( v = 0.6 \times 299,792,458 = 179,875,474.8 \) m/s.
- \( \gamma(v) = \frac{1}{\sqrt{1 - \frac{(0.6 \times 299,792,458)^2}{(299,792,458)^2}}} = \frac{1}{\sqrt{1 - 0.36}} = \frac{1}{\sqrt{0.64}} = 1.25 \)
- \( L = \frac{100}{1.25} = 80 \) m
- Result: \( L = 80.0000 \) m
Example 2: Calculate the observed length of a car with a proper length of 5 meters traveling at 100 km/h, with the result in centimeters:
- Enter \( L_0 = 5 \) m.
- Enter \( v = 100 \) km/h.
- Convert speed: \( v = 100 \times \frac{1000}{3600} = 27.7778 \) m/s.
- \( \gamma(v) = \frac{1}{\sqrt{1 - \frac{(27.7778)^2}{(299,792,458)^2}}} \approx 1.0000000000043 \)
- \( L = \frac{5}{1.0000000000043} \approx 5 \) m
- Convert to cm: \( L = 5 \times 100 = 500 \) cm
- Result: \( L = 500.0000 \) cm

5. Frequently Asked Questions (FAQ)

Q: What is length contraction?
A: Length contraction is a phenomenon in special relativity where the length of an object moving at relativistic speeds appears shorter to an observer at rest, compared to its proper length.

Q: Why does length contraction occur?
A: Length contraction occurs because, in special relativity, space and time are interconnected. As an object approaches the speed of light, its length contracts in the direction of motion to maintain the consistency of physical laws across different reference frames.

Q: Is length contraction noticeable at everyday speeds?
A: No, length contraction is negligible at everyday speeds because the effect becomes significant only at speeds close to the speed of light. For example, at 100 km/h, the contraction is extremely small.