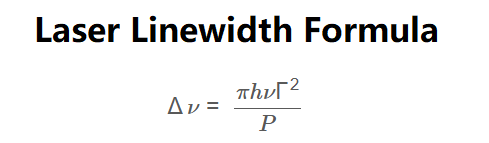Laser Linewidth Calculator

Fundamental Frequency (\( \nu \)):

Cavity Linewidth (\( \Delta \nu_{\text{cavity}} \)):

Laser Power (\( P \)):

1. What is Laser Linewidth Calculator?

Definition: This calculator computes the laser linewidth (\( \Delta \nu \)), which measures the spectral width of the laser's emission, indicating the range of frequencies present in the laser output.

Purpose: It is used in quantum optics and laser physics to determine the coherence and stability of a laser, which is critical for applications like spectroscopy, telecommunications, and precision measurements.

2. How Does the Calculator Work?

The calculator uses the formula for laser linewidth based on quantum mechanics:

Formula: \[ \Delta \nu = \frac{\pi h \nu \Gamma^2}{P} \]

\( \Delta \nu \): Laser linewidth (Hz, kHz, MHz, GHz, THz, RPM)
\( h \): Planck constant (\( 6.62607015 \times 10^{-34} \, \text{J·s} \))
\( \nu \): Fundamental frequency of the laser (Hz, kHz, MHz, GHz, THz, RPM)
\( \Delta \nu_{\text{cavity}} \): Cavity linewidth (Hz, kHz, MHz, GHz, THz, RPM)
\( \Gamma \): Q-factor of the laser cavity (dimensionless, calculated)
\( P \): Laser power (W, mW, kW)

Unit Conversions:

Frequency (\( \nu \)) and Cavity Linewidth (\( \Delta \nu_{\text{cavity}} \)): Hz, kHz (1 kHz = 1000 Hz), MHz (1 MHz = \( 10^6 \) Hz), GHz (1 GHz = \( 10^9 \) Hz), THz (1 THz = \( 10^{12} \) Hz), RPM (1 RPM = \( \frac{1}{60} \) Hz)
Power (\( P \)): W, mW (1 mW = 0.001 W), kW (1 kW = 1000 W)
Linewidth (\( \Delta \nu \)): Hz, kHz (1 kHz = 1000 Hz), MHz (1 MHz = \( 10^6 \) Hz), GHz (1 GHz = \( 10^9 \) Hz), THz (1 THz = \( 10^{12} \) Hz), RPM (1 RPM = \( \frac{1}{60} \) Hz)

Steps:

Enter the fundamental frequency (\( \nu \)), cavity linewidth (\( \Delta \nu_{\text{cavity}} \)), and laser power (\( P \)), and select their units.
Convert \( \nu \) and \( \Delta \nu_{\text{cavity}} \) to Hz, and \( P \) to watts.
Calculate the Q-factor using \( \Gamma = \frac{\nu}{\Delta \nu_{\text{cavity}}} \).
Calculate the linewidth using \( \Delta \nu = \frac{\pi h \nu \Gamma^2}{P} \).
Convert the result to the selected unit (Hz, kHz, MHz, GHz, THz, RPM).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Laser Linewidth Calculation

Calculating the linewidth of a laser is crucial for:

Spectroscopy: Narrow linewidths are essential for high-resolution measurements of atomic and molecular spectra.
Telecommunications: Low linewidths improve the performance of optical communication systems by reducing signal distortion.
Education: Understanding the quantum mechanical principles affecting laser performance, such as the uncertainty principle.

4. Using the Calculator

Examples:

Example 1: For \( \nu = 500 \, \text{THz} \), \( \Delta \nu_{\text{cavity}} = 5 \, \text{MHz} \), \( P = 1 \, \text{W} \), linewidth in Hz:
- Convert: \( \nu = 500 \times 10^{12} = 5 \times 10^{14} \, \text{Hz} \), \( \Delta \nu_{\text{cavity}} = 5 \times 10^6 = 5 \times 10^6 \, \text{Hz} \)
- Q-factor: \( \Gamma = \frac{5 \times 10^{14}}{5 \times 10^6} = 1 \times 10^8 \)
- Linewidth: \( \Delta \nu = \frac{\pi \times 6.62607015 \times 10^{-34} \times 5 \times 10^{14} \times (1 \times 10^8)^2}{1} \approx 1.0419 \times 10^7 \, \text{Hz} \)
Example 2: For \( \nu = 300 \, \text{GHz} \), \( \Delta \nu_{\text{cavity}} = 6 \, \text{kHz} \), \( P = 500 \, \text{mW} \), linewidth in kHz:
- Convert: \( \nu = 300 \times 10^9 = 3 \times 10^{11} \, \text{Hz} \), \( \Delta \nu_{\text{cavity}} = 6 \times 10^3 = 6 \times 10^3 \, \text{Hz} \), \( P = 500 \times 0.001 = 0.5 \, \text{W} \)
- Q-factor: \( \Gamma = \frac{3 \times 10^{11}}{6 \times 10^3} = 5 \times 10^7 \)
- Linewidth: \( \Delta \nu = \frac{\pi \times 6.62607015 \times 10^{-34} \times 3 \times 10^{11} \times (5 \times 10^7)^2}{0.5} \approx 3.1197 \times 10^6 \, \text{Hz} \)
- Convert to kHz: \( \Delta \nu = 3.1197 \times 10^6 \times 10^{-3} \approx 3.1197 \times 10^3 \, \text{kHz} \)

5. Frequently Asked Questions (FAQ)

Q: What is laser linewidth?
A: Laser linewidth (\( \Delta \nu \)) is the spectral width of the laser's emission, representing the range of frequencies present in the laser output. It indicates the laser's coherence and stability.

Q: How does the cavity linewidth affect the Q-factor?
A: The Q-factor (\( \Gamma \)) is inversely proportional to the cavity linewidth (\( \Delta \nu_{\text{cavity}} \)). A narrower cavity linewidth results in a higher Q-factor, indicating a more stable laser cavity.

Q: Why does higher power reduce linewidth?
A: The linewidth is inversely proportional to power (\( P \)). Higher power reduces the relative impact of quantum noise, leading to a narrower linewidth and a more coherent laser output.