Laser Beam Divergence Calculator

Initial Diameter (\( D_i \)):

Final Diameter (\( D_f \)):

Distance (\( l \)):

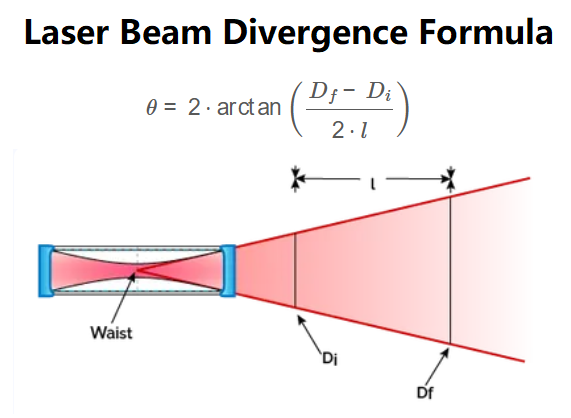
1. What is Laser Beam Divergence Calculator?

Definition: This calculator computes the divergence angle (\( \theta \)) of a laser beam, which measures how much the beam spreads as it propagates.

Purpose: It is used in optics to determine the spreading of a laser beam over a distance, essential for applications like laser communication, laser cutting, and beam focusing.

2. How Does the Calculator Work?

The calculator uses the formula for laser beam divergence:

Formula: \[ \theta = 2 \cdot \arctan\left(\frac{D_f - D_i}{2 \cdot l}\right) \] Where:

\( \theta \): Divergence angle (rad, deg, arcmin, arcsec, marcsec, μarcsec, mrad, μrad)
\( D_f \): Diameter of the beam at the final point (nm, μm, mm, cm, m, in, ft, yd)
\( D_i \): Diameter of the beam at the initial point (nm, μm, mm, cm, m, in, ft, yd)
\( l \): Distance between the initial and final points (nm, μm, mm, cm, m, km, mi, in, ft, yd)

Unit Conversions:

Diameters (\( D_i \), \( D_f \)) and Distance (\( l \)): nm (1 nm = \( 10^{-9} \) m), μm (1 μm = \( 10^{-6} \) m), mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, km (1 km = 1000 m), mi (1 mi = 1609.344 m), in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
Angle (\( \theta \)): rad, deg (1 deg = \( \frac{\pi}{180} \) rad), arcmin (1 arcmin = \( \frac{\pi}{180 \times 60} \) rad), arcsec (1 arcsec = \( \frac{\pi}{180 \times 3600} \) rad), marcsec (1 marcsec = \( \frac{\pi}{180 \times 3600 \times 1000} \) rad), μarcsec (1 μarcsec = \( \frac{\pi}{180 \times 3600 \times 10^6} \) rad), mrad (1 mrad = 0.001 rad), μrad (1 μrad = \( 10^{-6} \) rad)

Steps:

Enter the initial diameter (\( D_i \)), final diameter (\( D_f \)), and distance (\( l \)), and select their units.
Convert all inputs to meters.
Calculate the divergence angle using \( \theta = 2 \cdot \arctan\left(\frac{D_f - D_i}{2 \cdot l}\right) \).
Convert the result to the selected unit (rad, deg, arcmin, arcsec, marcsec, μarcsec, mrad, μrad).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Laser Beam Divergence Calculation

Calculating the divergence angle of a laser beam is crucial for:

Laser Applications: Ensuring precise beam focusing in laser cutting, welding, and medical procedures.
Communication: Designing laser-based communication systems where beam spread affects signal strength.
Education: Understanding the behavior of laser beams in optics and photonics.

4. Using the Calculator

Examples:

Example 1: For \( D_i = 2 \, \text{mm} \), \( D_f = 10 \, \text{mm} \), \( l = 100 \, \text{m} \), angle in degrees:
- Convert: \( D_i = 2 \times 0.001 = 0.002 \, \text{m} \), \( D_f = 10 \times 0.001 = 0.01 \, \text{m} \), \( l = 100 \, \text{m} \)
- Angle: \( \theta = 2 \cdot \arctan\left(\frac{0.01 - 0.002}{2 \times 100}\right) = 2 \cdot \arctan(0.00004) \approx 0.00008 \, \text{rad} \)
- Convert to degrees: \( \theta = 0.00008 \times \frac{180}{\pi} \approx 0.0046^\circ \)
Example 2: For \( D_i = 1 \, \text{cm} \), \( D_f = 5 \, \text{cm} \), \( l = 1 \, \text{km} \), angle in milliradians:
- Convert: \( D_i = 1 \times 0.01 = 0.01 \, \text{m} \), \( D_f = 5 \times 0.01 = 0.05 \, \text{m} \), \( l = 1 \times 1000 = 1000 \, \text{m} \)
- Angle: \( \theta = 2 \cdot \arctan\left(\frac{0.05 - 0.01}{2 \times 1000}\right) = 2 \cdot \arctan(0.00002) \approx 0.00004 \, \text{rad} \)
- Convert to milliradians: \( \theta = 0.00004 \times 1000 \approx 0.0400 \, \text{mrad} \)

5. Frequently Asked Questions (FAQ)

Q: What is laser beam divergence?
A: Laser beam divergence is the angle at which a laser beam spreads as it propagates, determined by the difference in beam diameters over a distance.

Q: Why is the divergence angle multiplied by 2 in the formula?
A: The formula measures the angle between the beam's edge and its propagation direction, which is half the total divergence. Multiplying by 2 gives the full divergence angle between the two edges of the beam.

Q: What does a smaller divergence angle indicate?
A: A smaller divergence angle indicates a more collimated (less spreading) beam, which is desirable for applications requiring a focused laser over long distances.