Lambert's Cosine Law Calculator

1. What is Lambert's Cosine Law Calculator?

Definition: This calculator determines the effective irradiance or illuminance on a surface based on the cosine of the incident angle, as per Lambert's Cosine Law.

Purpose: It is used in lighting design, photography, and phototherapy to account for the reduction in perceived light intensity at oblique angles.

2. How Does the Calculator Work?

The calculator uses the formula: \[ E_0 = E * \cos(\theta) \] Where:

\(E_0\): Effective irradiance at the incident angle (W/cm²)
\(E\): Initial irradiance perpendicular to the surface (W/cm²)
\(\theta\): Incident angle (radians)

Unit Conversions:

Angle: degrees, radians (1 degree = \( \pi/180 \) radians)
Irradiance: W/cm²

Steps:

Enter the initial irradiance (E) in W/cm².
Enter the incident angle (θ) and select its unit (degrees or radians).
Click "Calculate" to determine the effective irradiance (E₀) in W/cm².

3. Importance of Lambert's Cosine Law

Understanding this law is crucial for:

Lighting Design: Ensuring accurate light distribution on surfaces.
Photography: Adjusting exposure for angled light sources.
Phototherapy: Optimizing light delivery to human skin with cosine correction.

4. Using the Calculator

Examples:

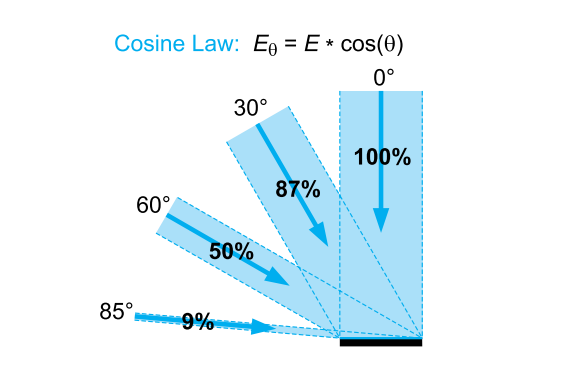
Example 1: Initial irradiance = 100 W/cm² at 30°:
- \(E_0 = 100 * \cos(30^\circ) = 100 * 0.866 = 86.6 \, \text{W/cm}^2\)
Example 2: Initial irradiance = 100 W/cm² at 60°:
- \(E_0 = 100 * \cos(60^\circ) = 100 * 0.5 = 50.0 \, \text{W/cm}^2\)

5. Frequently Asked Questions (FAQ)

Q: What is Lambert's Cosine Law?
A: It states that the irradiance on a surface varies as the cosine of the angle between the incident light and the surface normal.

Q: Why does irradiance decrease at an angle?
A: At oblique angles, the light spreads over a larger area, reducing the intensity per unit area.