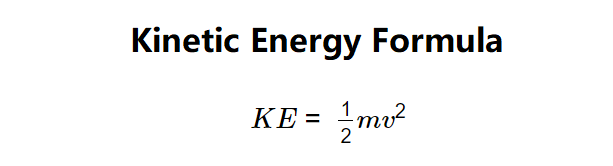Kinetic Energy Calculator

Mass (\( m \)):

Speed (\( v \)):

1. What is Kinetic Energy Calculator?

Definition: This calculator computes the classical (non-relativistic) kinetic energy (\( KE \)) of an object based on its mass (\( m \)) and speed (\( v \)).

Purpose: It is used in physics to determine the energy an object possesses due to its motion, applicable in scenarios like moving vehicles, projectiles, or any object in motion at low speeds.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula:

\( KE = \frac{1}{2} m v^2 \)

Where:

\( KE \): Kinetic energy (J, kJ, MJ, eV, keV, MeV)
\( m \): Mass of the object (kg, g, lb, oz)
\( v \): Speed of the object (m/s, km/h, mph, ft/s)

Unit Conversions:

Mass (\( m \)):
- 1 kg = 1 kg
- 1 g = \( 10^{-3} \) kg
- 1 lb = 0.453592 kg
- 1 oz = 0.0283495 kg
Speed (\( v \)):
- 1 m/s = 1 m/s
- 1 km/h = \( \frac{1000}{3600} \) m/s
- 1 mph = \( \frac{1609.344}{3600} \) m/s
- 1 ft/s = 0.3048 m/s
Energy (\( KE \)):
- 1 J = 1 J
- 1 kJ = \( 10^3 \) J
- 1 MJ = \( 10^6 \) J
- 1 eV = \( 1.602 \times 10^{-19} \) J
- 1 keV = \( 1.602 \times 10^{-16} \) J
- 1 MeV = \( 1.602 \times 10^{-13} \) J

Steps:

Enter the mass (\( m \)) with its respective unit (kg, g, lb, oz).
Enter the speed (\( v \)) with its respective unit (m/s, km/h, mph, ft/s).
Convert the mass to kilograms and the speed to meters per second.
Calculate the kinetic energy using \( KE = \frac{1}{2} m v^2 \).
Select the desired unit for the energy result (J, kJ, MJ, eV, keV, MeV).
Convert the energy to the selected unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Kinetic Energy Calculation

Calculating kinetic energy is crucial for:

Physics and Engineering: It helps in understanding the energy of moving objects, such as vehicles, projectiles, or machinery, for design and safety analysis.
Collision Analysis: Kinetic energy is a key factor in determining the impact energy during collisions, useful in automotive safety and accident reconstruction.
Education: It introduces students to the concept of energy in classical mechanics, illustrating the relationship between mass, speed, and energy.

4. Using the Calculator

Examples:

Example 1: Calculate the kinetic energy of a 1000 kg car traveling at 60 km/h, with the result in joules:
- Enter \( m = 1000 \) kg.
- Enter \( v = 60 \) km/h.
- Convert speed: \( v = 60 \times \frac{1000}{3600} = 16.6667 \) m/s.
- \( KE = \frac{1}{2} \times 1000 \times (16.6667)^2 \approx 138,888.8889 \) J
- Result: \( KE = 138888.8889 \) J
Example 2: Calculate the kinetic energy of a 500 g ball traveling at 20 m/s, with the result in kJ:
- Enter \( m = 500 \) g.
- Convert mass: \( m = 500 \times 10^{-3} = 0.5 \) kg.
- Enter \( v = 20 \) m/s.
- \( KE = \frac{1}{2} \times 0.5 \times (20)^2 = 100 \) J
- Convert to kJ: \( KE = 100 / 1000 = 0.1 \) kJ
- Result: \( KE = 0.1000 \) kJ

5. Frequently Asked Questions (FAQ)

Q: What is kinetic energy?
A: Kinetic energy is the energy an object possesses due to its motion, calculated as \( KE = \frac{1}{2} m v^2 \) in classical (non-relativistic) physics.

Q: Why is this calculation non-relativistic?
A: The formula \( KE = \frac{1}{2} m v^2 \) is valid for low speeds (much less than the speed of light). For high speeds, a relativistic formula must be used to account for effects like mass increase.

Q: What happens if the speed is very high?
A: The calculator will display an error if the speed exceeds the speed of light, as this formula is not valid for relativistic speeds. For high speeds, you should use a relativistic kinetic energy calculator.