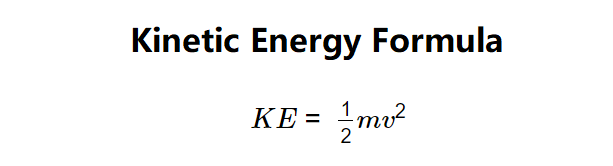Kinetic Energy Calculator Without Velocity

Kinetic Energy (KE):

Mass (m):

1. What is a Speed Calculator?

Definition: This calculator determines the speed (velocity) of an object based on its kinetic energy and mass, using the relationship derived from the kinetic energy formula.

Purpose: It is used in physics to calculate the speed of a moving object when its kinetic energy and mass are known, applicable in contexts like vehicle dynamics, collision analysis, and motion studies.

2. How Does the Calculator Work?

The calculator uses the following formula, derived from \( KE = \frac{1}{2} m v^2 \):

\[ v = \sqrt{\frac{2 \cdot KE}{m}} \] Where:

\( v \): Speed (m/s, km/h, ft/s, mph, kn, ft/min)
\( KE \): Kinetic energy (J, kJ, MJ, Wh, kWh, ft-lb, kcal)
\( m \): Mass (μg, mg, g, dag, kg, t, gr, dr, oz, lb, st)

Unit Conversions:

Kinetic Energy (KE): J, kJ (1 kJ = 1000 J), MJ (1 MJ = 1000000 J), Wh (1 Wh = 3600 J), kWh (1 kWh = 3600000 J), ft-lb (1 ft-lb = 1/0.73756214927727 J), kcal (1 kcal = 4184 J)
Mass (m): μg (1 μg = 0.000000001 kg), mg (1 mg = 0.000001 kg), g (1 g = 0.001 kg), dag (1 dag = 0.01 kg), kg, t (1 t = 1000 kg), gr (1 gr = 0.00006479891 kg), dr (1 dr = 0.0017718452 kg), oz (1 oz = 0.028349523 kg), lb (1 lb = 0.45359237 kg), st (1 st = 6.35029318 kg)
Speed (v): m/s, km/h (1 m/s = 3.6 km/h), ft/s (1 m/s = 1/0.3048 ft/s), mph (1 m/s = 1/0.44704 mph), kn (1 m/s = 1/0.514444 kn), ft/min (1 m/s = 60/0.3048 ft/min)

Steps:

Enter the kinetic energy (KE), selecting the unit (J, kJ, MJ, Wh, kWh, ft-lb, kcal).
Enter the mass (m), selecting the unit (μg, mg, g, dag, kg, t, gr, dr, oz, lb, st).
Convert inputs to base units (J for energy, kg for mass).
Calculate the speed using the formula \( v = \sqrt{\frac{2 \cdot KE}{m}} \).
Convert the result to the selected speed unit and display, using scientific notation for values < 0.0001 or > 10,000.

3. Importance of Speed Calculation

Calculating speed from kinetic energy and mass is crucial for:

Physics Education: Understanding the relationship between energy and motion.
Engineering: Analyzing the velocity of objects in mechanical systems or collisions.
Safety Analysis: Estimating speeds in accident reconstructions or impact studies.

4. Using the Calculator

Examples:

Example 1 (Car): For \( KE = 25 \, \text{J} \), \( m = 2 \, \text{kg} \):
- Speed: \( v = \sqrt{\frac{2 \cdot 25}{2}} = \sqrt{25} = 5 \, \text{m/s} \)
- In km/h: \( v = 5 \times 3.6 = 18 \, \text{km/h} \)
- In mph: \( v = 5 \times (1/0.44704) \approx 11.185 \, \text{mph} \)
- Result (within 0.0001–10,000): 5.000 m/s, 18.000 km/h, 11.185 mph
Example 2 (Small Object): For \( KE = 5 \, \text{J} \), \( m = 100 \, \text{g} \):
- Convert: \( m = 100 \times 0.001 = 0.1 \, \text{kg} \)
- Speed: \( v = \sqrt{\frac{2 \cdot 5}{0.1}} = \sqrt{100} = 10 \, \text{m/s} \)
- In ft/s: \( v = 10 \times (1/0.3048) \approx 32.808 \, \text{ft/s} \)
- In kn: \( v = 10 \times (1/0.514444) \approx 19.438 \, \text{kn} \)
- Result (within 0.0001–10,000): 10.000 m/s, 32.808 ft/s, 19.438 kn
Example 3 (Large Object): For \( KE = 1 \, \text{MJ} \), \( m = 1000 \, \text{kg} \):
- Convert: \( KE = 1 \times 1000000 = 1000000 \, \text{J} \)
- Speed: \( v = \sqrt{\frac{2 \cdot 1000000}{1000}} = \sqrt{2000} \approx 44.721 \, \text{m/s} \)
- In km/h: \( v = 44.721 \times 3.6 \approx 161.000 \, \text{km/h} \)
- In ft/min: \( v = 44.721 \times (60/0.3048) \approx 8808.465 \, \text{ft/min} \)
- Result (within 0.0001–10,000): 44.721 m/s, 161.000 km/h, 8808.465 ft/min

5. Frequently Asked Questions (FAQ)

Q: What is the speed calculator?
A: The speed calculator determines the velocity of an object based on its kinetic energy and mass, using the formula \( v = \sqrt{\frac{2 \cdot KE}{m}} \).

Q: Can the calculated speed be negative?
A: No, the speed calculated here is a magnitude (scalar), always non-negative, as it is derived from the square root of a positive quantity.

Q: Why do some results use scientific notation?
A: Results less than 0.0001 or greater than 10,000 are displayed in scientific notation to improve readability for very small or large speeds.

Q: What happens if kinetic energy is zero?
A: If kinetic energy is zero, the speed is also zero, as the object has no motion.

Q: Why must mass be positive?
A: Mass must be positive to avoid division by zero in the formula and because physical objects have positive mass.