1. What is the Kinematic Viscosity of Air Calculator?
Definition: This calculator computes the density (\( \rho \)), dynamic viscosity (\( \mu \)), and kinematic viscosity (\( \nu \)) of air based on the pressure, temperature, and specific gas constant of the air. Kinematic viscosity describes the resistance of air to flow due to internal friction, accounting for its density.
Purpose: It is used in aerodynamics, fluid dynamics, and engineering to analyze air flow in applications like aircraft design, HVAC systems, and wind tunnel testing.
2. How Does the Calculator Work?
The calculator uses the following formulas:
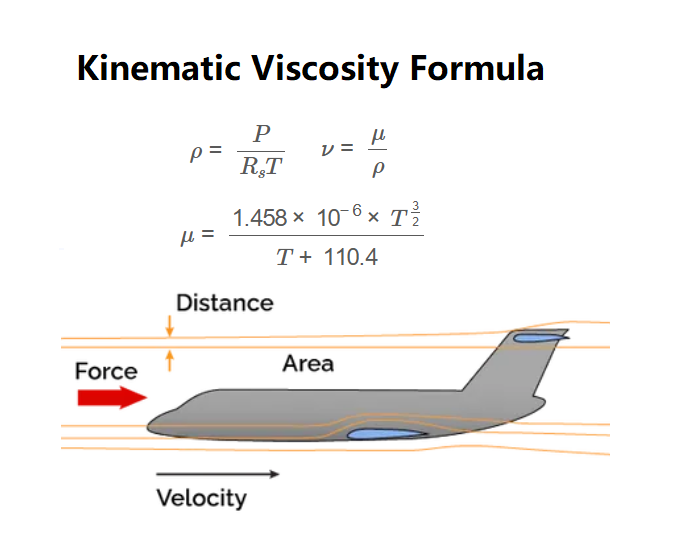
Formulas:
\[
\rho = \frac{P}{R_s T}
\]
\[
\mu = \frac{1.458 \times 10^{-6} \times T^{\frac{3}{2}}}{T + 110.4}
\]
\[
\nu = \frac{\mu}{\rho}
\]
where:
- \( \rho \): Density (kg/m³, g/m³, lb/ft³)
- \( \mu \): Dynamic viscosity (kg/m·s, Pa·s, cP)
- \( \nu \): Kinematic viscosity (m²/s, St, cSt, mm²/s)
- \( P \): Absolute pressure (Pa, bar, psi, at, atm, Torr, hPa, kPa, lb/ft², mmHg, inHg)
- \( R_s \): Specific gas constant (J/(kg·K))
- \( T \): Absolute temperature (K, °C, °F)
Unit Conversions:
- Pressure (\( P \)):
- 1 Pa = 1 Pa
- 1 bar = 100000 Pa
- 1 psi = 6894.76 Pa
- 1 at = 98066.5 Pa
- 1 atm = 101325 Pa
- 1 Torr = 133.322 Pa
- 1 hPa = 100 Pa
- 1 kPa = 1000 Pa
- 1 lb/ft² = 47.8803 Pa
- 1 mmHg = 133.322 Pa
- 1 inHg = 3386.39 Pa
- Temperature (\( T \)):
- 1 °C = T + 273.15 K
- 1 °F = (T - 32) × 5/9 + 273.15 K
- 1 K = 1 K
- Density (\( \rho \)):
- 1 kg/m³ = 1 kg/m³
- 1 g/m³ = 0.001 kg/m³
- 1 lb/ft³ = 16.0185 kg/m³
- Dynamic Viscosity (\( \mu \)):
- 1 kg/m·s = 1 kg/m·s
- 1 Pa·s = 1 kg/m·s
- 1 cP = 0.001 Pa·s
- Kinematic Viscosity (\( \nu \)):
- 1 m²/s = 1 m²/s
- 1 St = 1e-4 m²/s
- 1 cSt = 1e-6 m²/s
- 1 mm²/s = 1e-6 m²/s
Steps:
- Enter the pressure in Pa, bar, psi, at, atm, Torr, hPa, kPa, lb/ft², mmHg, or inHg (default is 101325 Pa, step size 0.00001).
- Enter the temperature in °C, °F, or K (default is 25°C, step size 0.00001).
- Enter the specific gas constant in J/(kg·K) (default is 287.05 J/(kg·K), step size 0.00001).
- Convert pressure to Pa and temperature to Kelvin (K).
- Calculate the density (\( \rho \)) using the ideal gas law.
- Calculate the dynamic viscosity (\( \mu \)) using the empirical formula.
- Calculate the kinematic viscosity (\( \nu \)) by dividing dynamic viscosity by density.
- Convert the results to the selected units and display them, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.
3. Importance of Kinematic Viscosity of Air Calculation
Calculating the kinematic viscosity of air is crucial for:
- Aerodynamics: Understanding air flow over aircraft surfaces, which affects lift, drag, and fuel efficiency.
- Fluid Dynamics: Analyzing the behavior of air in pipes, ducts, and wind tunnels for engineering applications.
- HVAC Systems: Designing efficient ventilation and air conditioning systems by accounting for air flow resistance.
4. Using the Calculator
Examples:
- Example 1: Calculate the density, dynamic viscosity, and kinematic viscosity of air with a pressure of 101325 Pa, temperature of 25°C, and specific gas constant of 287.05 J/(kg·K), with density in kg/m³, dynamic viscosity in kg/m·s, and kinematic viscosity in m²/s:
- Enter Pressure = 101325 Pa.
- Enter Temperature = 25 °C, convert to K: \( 25 + 273.15 = 298.15 \, \text{K} \).
- Enter Specific Gas Constant = 287.05 J/(kg·K).
- Density: \( \rho = \frac{101325}{287.05 \times 298.15} = 1.1839 \, \text{kg/m}^3 \).
- Dynamic viscosity: \( \mu = \frac{1.458 \times 10^{-6} \times 298.15^{\frac{3}{2}}}{298.15 + 110.4} = \frac{1.458 \times 10^{-6} \times 5147.93}{408.55} = 1.8366 \times 10^{-5} \, \text{kg/m·s} \).
- Kinematic viscosity: \( \nu = \frac{1.8366 \times 10^{-5}}{1.1839} = 1.5518 \times 10^{-5} \, \text{m}^2/\text{s} \).
- Result: \( \rho = 1.1839 \, \text{kg/m}^3 \), \( \mu = 1.8366 \times 10^{-5} \, \text{kg/m·s} \), \( \nu = 1.5518 \times 10^{-5} \, \text{m}^2/\text{s} \).
- Example 2: Calculate the density, dynamic viscosity, and kinematic viscosity of air with a pressure of 29.92 inHg, temperature of 86°F, and specific gas constant of 287.05 J/(kg·K), with density in lb/ft³, dynamic viscosity in cP, and kinematic viscosity in cSt:
- Enter Pressure = 29.92 inHg, convert to Pa: \( 29.92 \times 3386.39 = 101283.99 \, \text{Pa} \).
- Enter Temperature = 86 °F, convert to K: \( (86 - 32) \times 5/9 + 273.15 = 303.15 \, \text{K} \).
- Enter Specific Gas Constant = 287.05 J/(kg·K).
- Density: \( \rho = \frac{101283.99}{287.05 \times 303.15} = 1.1639 \, \text{kg/m}^3 \).
- Convert to lb/ft³: \( 1.1639 \times 62.428 = 72.6507 \).
- Dynamic viscosity: \( \mu = \frac{1.458 \times 10^{-6} \times 303.15^{\frac{3}{2}}}{303.15 + 110.4} = \frac{1.458 \times 10^{-6} \times 5279.92}{413.55} = 1.8614 \times 10^{-5} \, \text{kg/m·s} \).
- Convert to cP: \( 1.8614 \times 10^{-5} \times 1000 = 0.0186 \).
- Kinematic viscosity: \( \nu = \frac{1.8614 \times 10^{-5}}{1.1639} = 1.5991 \times 10^{-5} \, \text{m}^2/\text{s} \).
- Convert to cSt: \( 1.5991 \times 10^{-5} \times 1e6 = 15.991 \).
- Result: \( \rho = 72.6507 \, \text{lb/ft}^3 \), \( \mu = 0.0186 \, \text{cP} \), \( \nu = 15.9910 \, \text{cSt} \).
5. Frequently Asked Questions (FAQ)
Q: What is kinematic viscosity?
A: Kinematic viscosity (\( \nu \)) is the ratio of dynamic viscosity (\( \mu \)) to density (\( \rho \)), describing the resistance of a fluid to flow under gravity. For air, it is a key parameter in fluid dynamics and aerodynamics.
Q: Why does temperature affect viscosity?
A: As temperature increases, the molecular activity in air increases, reducing the internal friction (dynamic viscosity increases slightly, but density decreases more significantly), leading to a higher kinematic viscosity.
Q: What is the specific gas constant for air?
A: The specific gas constant for dry air (\( R_s \)) is typically 287.05 J/(kg·K). This value is used in the ideal gas law to calculate air density, but the calculator allows users to input a custom value for flexibility.
Kinematic Viscosity of Air Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back