Isentropic Flow Calculator

Specific Heat Ratio (\( \gamma \)):

Gas Constant (\( R \)):

Stagnation Pressure (\( P_0 \)):

Stagnation Temperature (\( T_0 \)):

Flow Velocity (\( c \)):

Stagnation Density (\( \rho_0 \)):

Speed of Sound (\( a_0 \)):

Mach Number (\( M \)):

Pressure Ratio (\( P/P_0 \)):

Temperature Ratio (\( T/T_0 \)):

Density Ratio (\( \rho/\rho_0 \)):

Critical Pressure Ratio (\( P^*/P_0 \)):

Critical Temperature Ratio (\( T^*/T_0 \)):

Critical Density Ratio (\( \rho^*/\rho_0 \)):

Critical Pressure (\( P^* \)):

Critical Temperature (\( T^* \)):

Critical Density (\( \rho^* \)):

Static Pressure (\( P \)):

Static Temperature (\( T \)):

Static Density (\( \rho \)):

1. What is Isentropic Flow Calculator?

Definition: This calculator computes the properties of an isentropic flow process, an adiabatic and reversible flow where entropy remains constant, using the flow velocity, stagnation pressure, and temperature to determine the Mach number, flow ratios, and absolute flow properties.

Purpose: It helps engineers and students analyze compressible flows in high-velocity gas systems, such as jet engines and nozzles, by calculating key flow parameters, ratios, and absolute properties.

2. How Does the Calculator Work?

The calculator uses the following equations for a perfect gas:

Stagnation Density: \( \rho_0 = \frac{P_0}{R T_0} \)
Speed of Sound: \( a_0 = \sqrt{\gamma R T_0} \)
Mach Number: \( M = \frac{c}{a_0} \)
Temperature Ratio: \( \frac{T}{T_0} = \frac{1}{1 + \frac{\gamma - 1}{2} M^2} \)
Pressure Ratio: \( \frac{P}{P_0} = \left( \frac{T}{T_0} \right)^{\frac{\gamma}{\gamma - 1}} \)
Density Ratio: \( \frac{\rho}{\rho_0} = \left( \frac{T}{T_0} \right)^{\frac{1}{\gamma - 1}} \)
Critical Temperature Ratio (\( M = 1 \)): \( \frac{T^*}{T_0} = \frac{2}{\gamma + 1} \)
Critical Properties: \( P^* = \frac{P^*}{P_0} \cdot P_0 \), \( T^* = \frac{T^*}{T_0} \cdot T_0 \), \( \rho^* = \frac{\rho^*}{\rho_0} \cdot \rho_0 \)
Static Properties: \( P = \frac{P}{P_0} \cdot P_0 \), \( T = \frac{T}{T_0} \cdot T_0 \), \( \rho = \frac{\rho}{\rho_0} \cdot \rho_0 \)

Where:

\( \gamma \): Specific heat ratio;
\( R \): Gas constant (J/(kg·K));
\( P_0 \): Stagnation pressure (Pa);
\( T_0 \): Stagnation temperature (K);
\( \rho_0 \): Stagnation density (kg/m³);
\( c \): Flow velocity (m/s);
\( a_0 \): Speed of sound at stagnation conditions (m/s);
\( M \): Mach number;
\( P, T, \rho \): Static pressure, temperature, and density;
\( P^*, T^*, \rho^* \): Critical properties at \( M = 1 \).

Steps:

Enter the specific heat ratio (\( \gamma \)), typically 1.4 for air.
Enter the gas constant (\( R \)), typically 287 J/(kg·K) for air, with its unit.
Enter the stagnation pressure (\( P_0 \)) and its unit.
Enter the stagnation temperature (\( T_0 \)) and its unit.
Enter the flow velocity (\( c \)) and its unit.
Convert all inputs to base units (J/(kg·K) for \( R \), Pa for pressure, K for temperature, m/s for velocity).
Calculate the stagnation density (\( \rho_0 \)) using the ideal gas law.
Calculate the speed of sound (\( a_0 \)) at stagnation conditions.
Calculate the Mach number (\( M \)) using \( M = c / a_0 \).
Calculate the isentropic flow ratios and critical ratios.
Compute absolute critical and static properties using the ratios and stagnation values.
Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Isentropic Flow Calculation

Calculating isentropic flow properties is crucial for:

Aerospace Engineering: Designing nozzles and diffusers in jet engines and rockets where isentropic assumptions simplify analysis.
Gas Dynamics: Understanding compressible flow behavior in high-speed applications like turbines and compressors.
Thermodynamic Analysis: Evaluating ideal performance of systems to compare with real-world efficiencies.

4. Using the Calculator

Example 1 (Air at Standard Conditions): Calculate the flow properties for air with the following inputs:

Specific Heat Ratio: \( \gamma = 1.4 \);
Gas Constant: \( R = 287 \, \text{J/(kg·K)} \);
Stagnation Pressure: \( P_0 = 101325 \, \text{Pa} \);
Stagnation Temperature: \( T_0 = 300 \, \text{K} \);
Flow Velocity: \( c = 170.61 \, \text{m/s} \);
Stagnation Density: \( \rho_0 = \frac{101325}{287 \times 300} \approx 1.1774 \, \text{kg/m}^3 \);
Speed of Sound: \( a_0 = \sqrt{1.4 \times 287 \times 300} \approx 347.21 \, \text{m/s} \);
Mach Number: \( M = \frac{170.61}{347.21} \approx 0.4914 \);
Temperature Ratio: \( \frac{T}{T_0} = \frac{1}{1 + \frac{1.4 - 1}{2} \times 0.4914^2} \approx 0.9537 \);
Pressure Ratio: \( \frac{P}{P_0} = (0.9537)^{\frac{1.4}{1.4 - 1}} \approx 0.8469 \);
Density Ratio: \( \frac{\rho}{\rho_0} = (0.9537)^{\frac{1}{1.4 - 1}} \approx 0.8880 \);
Critical Pressure: \( P^* = 0.5283 \times 101325 \approx 53527.58 \, \text{Pa} \);
Critical Temperature: \( T^* = 0.8333 \times 300 \approx 250.00 \, \text{K} \);
Critical Density: \( \rho^* = 0.6339 \times 1.1774 \approx 0.7464 \, \text{kg/m}^3 \);
Static Pressure: \( P = 0.8469 \times 101325 \approx 85814.31 \, \text{Pa} \);
Static Density: \( \rho = 0.8880 \times 1.1774 \approx 1.0455 \, \text{kg/m}^3 \);
Result: \( \rho_0 = 1.1774 \, \text{kg/m}^3 \), \( a_0 = 347.21 \, \text{m/s} \), \( M = 0.4914 \), \( P^* = 53527.58 \, \text{Pa} \), \( T^* = 250.00 \, \text{K} \), \( \rho^* = 0.7464 \, \text{kg/m}^3 \), \( P = 85814.31 \, \text{Pa} \), \( \rho = 1.0455 \, \text{kg/m}^3 \).

Example 2 (Different Gas and Units): Calculate the flow properties with the following inputs:

Specific Heat Ratio: \( \gamma = 1.3 \);
Gas Constant: \( R = 0.287 \, \text{J/(g·K)} \);
Stagnation Pressure: \( P_0 = 1.01325 \, \text{bar} \);
Stagnation Temperature: \( T_0 = 27 \, \text{°C} \);
Flow Velocity: \( c = 200 \, \text{km/h} \);
Convert units: \( R = 0.287 \times 1000 = 287 \, \text{J/(kg·K)} \), \( P_0 = 1.01325 \times 10^5 = 101325 \, \text{Pa} \), \( T_0 = 27 + 273.15 = 300.15 \, \text{K} \), \( c = 200 \times \frac{1000}{3600} \approx 55.56 \, \text{m/s} \);
Stagnation Density: \( \rho_0 \approx 1.1765 \, \text{kg/m}^3 \);
Speed of Sound: \( a_0 \approx 334.81 \, \text{m/s} \);
Mach Number: \( M \approx 0.1659 \);
Critical Pressure: \( P^* = 0.5457 \times 101325 \approx 55292.99 \, \text{Pa} \);
Critical Temperature: \( T^* = 0.8696 \times 300.15 \approx 261.01 \, \text{K} \);
Static Pressure: \( P = 0.9819 \times 101325 \approx 99488.85 \, \text{Pa} \);
Result: \( \rho_0 = 1.1765 \, \text{kg/m}^3 \), \( a_0 = 1205.32 \, \text{km/h} \), \( M = 0.1659 \), \( P^* = 0.5529 \, \text{bar} \), \( T^* = -12.14 \, \text{°C} \), \( P = 0.9949 \, \text{bar} \).

5. Frequently Asked Questions (FAQ)

Q: What is an isentropic flow?
A: An isentropic flow is an adiabatic and reversible flow where entropy remains constant, often used as an ideal model in gas dynamics for high-velocity flows.

Q: Why is the specific heat ratio (\( \gamma \)) important?
A: The specific heat ratio determines how the gas responds to compression and expansion, affecting the relationships between pressure, temperature, and density in isentropic flow.

Q: What are critical properties?
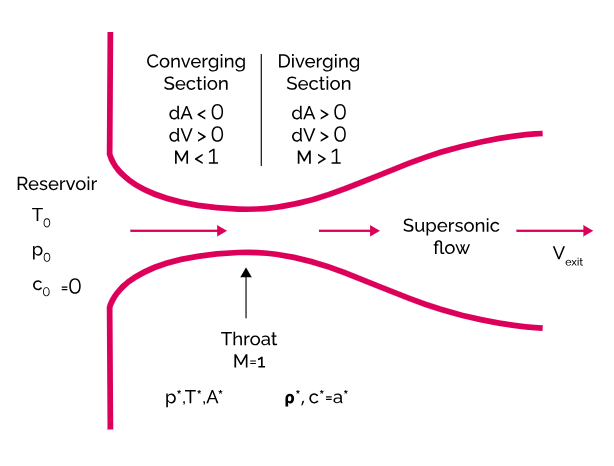
A: Critical properties (\( P^* \), \( T^* \), \( \rho^* \)) occur at \( M = 1 \), typically at the throat of a converging-diverging nozzle, where the flow reaches sonic conditions.