Inverse Square Law Calculator

Intensity at Distance 1 (\( I_1 \)):

× 10^

Intensity at Distance 2 (\( I_2 \)):

× 10^

Distance 1 (\( r_1 \)):

1. What is the Inverse Square Law Calculator?

Definition: This calculator computes the distance (\( r_2 \)) at which a given intensity (\( I_2 \)) is observed, given the intensity (\( I_1 \)) at distance (\( r_1 \)), using the inverse square law.

Purpose: It is used in physics to determine the distance at which a specific intensity (e.g., light, sound, radiation) is achieved from a point source, such as a light bulb or a radioactive source.

2. How Does the Calculator Work?

The calculator uses the inverse square law equation:

\( \frac{I_1}{I_2} = \frac{r_2^2}{r_1^2} \)

Rearranged to solve for \( r_2 \):

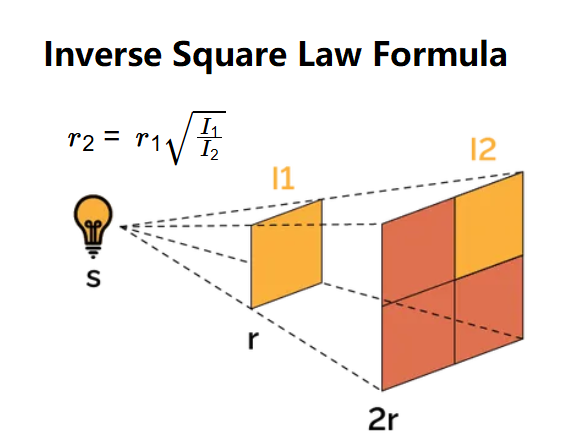
\( r_2 = r_1 \sqrt{\frac{I_1}{I_2}} \)

Where:

\( I_1 \): Intensity at distance \( r_1 \) (unitless, with a base value × 10^exponent);
\( I_2 \): Intensity at distance \( r_2 \) (unitless, with a base value × 10^exponent);
\( r_1 \): Distance 1 (cm, m, km, in, ft, yd, mi);
\( r_2 \): Distance 2 (cm, m, km, in, ft, yd, mi).

Steps:

Enter the intensity at distance 1 (\( I_1 \)) as a base value and exponent (e.g., 5 × 10^3).
Enter the intensity at distance 2 (\( I_2 \)) as a base value and exponent.
Enter distance 1 (\( r_1 \)) with its unit.
Select the desired unit for distance 2 (\( r_2 \)).
Convert the distance \( r_1 \) to base units (meters).
Calculate the intensities by multiplying the base values by their respective powers of 10.
Calculate distance 2: \( r_2 = r_1 \sqrt{\frac{I_1}{I_2}} \).
Convert the result to the selected unit for \( r_2 \) and display \( r_2 \), formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Inverse Square Law Calculation

Calculating distance using the inverse square law is crucial for:

Lighting Design: Determining the distance at which a desired light intensity is achieved.
Radiation Safety: Estimating safe distances for a given radiation exposure level.
Acoustics: Finding the distance at which a specific sound intensity is heard.

4. Using the Calculator

Example 1 (Light Intensity): Find the distance at which the light intensity is 25 lux, given an intensity of 100 lux at 1 meter:

Intensity at Distance 1: \( I_1 = 100 \times 10^0 = 100 \, \text{lux} \);
Intensity at Distance 2: \( I_2 = 25 \times 10^0 = 25 \, \text{lux} \);
Distance 1: \( r_1 = 1 \, \text{m} \);
Distance 2: \( r_2 = 1 \times \sqrt{\frac{100}{25}} = 1 \times \sqrt{4} = 2 \, \text{m} \);
Result (in meters): \( r_2 = 2.0000 \, \text{m} \);
Result (in feet): \( r_2 = 2 \times 3.28084 = 6.5617 \, \text{ft} \).

Example 2 (Radiation Intensity): Find the distance at which the radiation intensity is \( 1 \times 10^{-3} \, \text{W/m}^2 \), given an intensity of \( 0.1 \times 10^0 \, \text{W/m}^2 \) at 1 km:

Intensity at Distance 1: \( I_1 = 0.1 \times 10^0 = 0.1 \, \text{W/m}^2 \);
Intensity at Distance 2: \( I_2 = 1 \times 10^{-3} = 0.001 \, \text{W/m}^2 \);
Distance 1: \( r_1 = 1 \, \text{km} = 1000 \, \text{m} \);
Distance 2: \( r_2 = 1000 \times \sqrt{\frac{0.1}{0.001}} = 1000 \times \sqrt{100} = 1000 \times 10 = 10,000 \, \text{m} \);
Result (in kilometers): \( r_2 = 10,000 \times 10^{-3} = 10.0000 \, \text{km} \);
Result (in miles): \( r_2 = 10,000 \times 0.000621371 = 6.2137 \, \text{mi} \).

5. Frequently Asked Questions (FAQ)

Q: What does the inverse square law apply to?
A: It applies to any quantity that spreads out from a point source, such as light, sound, gravitational force, or radiation, assuming no absorption or scattering.

Q: Why does intensity decrease with the square of the distance?
A: The energy from a point source spreads over the surface of a sphere, and the surface area of a sphere increases with the square of the radius (\( 4\pi r^2 \)), so the intensity decreases as \( 1/r^2 \).

Q: Does this calculator account for absorption or scattering?
A: No, this calculator assumes ideal conditions with no absorption, scattering, or other losses. In real-world scenarios, these factors may reduce intensity further.