Immersed Weight Calculator

Object weight:

Object volume:

1. What is the Immersed Weight Calculator?

Definition: This calculator computes the immersed weight of an object submerged in various fluids, accounting for the buoyant force exerted by each fluid, using Archimedes' principle.

Purpose: It helps understand how an object's effective weight changes in different fluids, useful for educational experiments, engineering applications, and determining whether an object will float or sink.

2. How Does the Calculator Work?

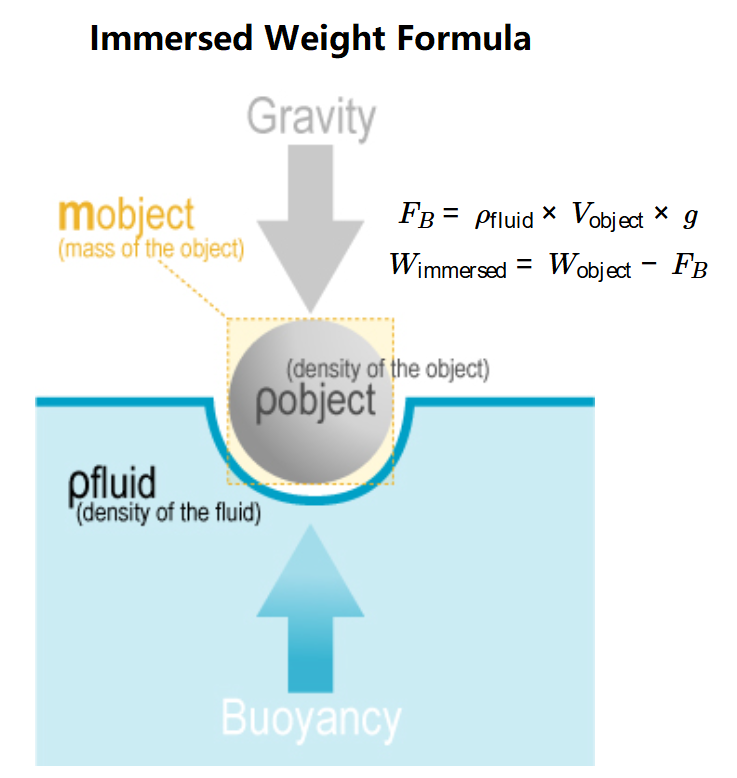
The calculator uses the following equations:

\( F_B = \rho_{\text{fluid}} \times V_{\text{object}} \times g \)
\( W_{\text{immersed}} = W_{\text{object}} - F_B \)

Where:

\( F_B \): Buoyant force (N);
\( \rho_{\text{fluid}} \): Density of the fluid (kg/m³);
\( V_{\text{object}} \): Volume of the object (converted to m³);
\( g \): Gravitational acceleration (fixed at 9.81 m/s²);
\( W_{\text{immersed}} \): Immersed weight (converted to selected mass unit);
\( W_{\text{object}} \): Weight of the object in air (converted to N).

Steps:

Enter the weight of the object with its unit.
Enter the volume of the object with its unit.
Convert weight to Newtons (via kg) and volume to m³.
For each fluid, calculate the buoyant force: \( F_B = \rho_{\text{fluid}} \times V_{\text{object}} \times g \).
Calculate the immersed weight in Newtons: \( W_{\text{immersed}} = W_{\text{object}} - F_B \).
Convert the immersed weight to the selected output mass unit for each fluid.
Display the immersed weight for each fluid, noting that negative values indicate the object will float.

3. Importance of Immersed Weight Calculation

Calculating the immersed weight is crucial for:

Physics Education: Demonstrating Archimedes' principle and the concept of buoyancy through experiments.
Engineering: Designing boats, submarines, and other structures that interact with fluids.
Material Science: Understanding how objects behave in different liquids based on their density.

4. Using the Calculator

Example 1 (Matching Image): Calculate the immersed weight of an object in various fluids:

Object Weight: \( W_{\text{object}} = 1 \, \text{lb} \), converted to \( 0.453592 \, \text{kg} \), then to \( 0.453592 \times 9.81 = 4.44994 \, \text{N} \);
Object Volume: \( V_{\text{object}} = 1 \, \text{cm}^3 = 10^{-6} \, \text{m}^3 \);
In Gasoline: \( F_B = 737 \times 10^{-6} \times 9.81 = 0.00723 \, \text{N} \), \( W_{\text{immersed}} = 4.44994 - 0.00723 = 4.44271 \, \text{N} \), in oz: \( (4.44271 / 9.81) \times 2.20462 \times 16 = 15.98 \, \text{oz} \), in mg: \( (4.44271 / 9.81) \times 1e6 = 452895.62 \, \text{mg} \);
In Mercury: \( F_B = 13560 \times 10^{-6} \times 9.81 = 0.13300 \, \text{N} \), \( W_{\text{immersed}} = 4.44994 - 0.13300 = 4.31694 \, \text{N} \), in oz: \( (4.31694 / 9.81) \times 2.20462 \times 16 = 15.52 \, \text{oz} \), in mg: \( (4.31694 / 9.81) \times 1e6 = 440152.91 \, \text{mg} \).

Example 2: Calculate the immersed weight using different units:

Object Weight: \( W_{\text{object}} = 500 \, \text{g} = 0.5 \, \text{kg} \), converted to \( 0.5 \times 9.81 = 4.905 \, \text{N} \);
Object Volume: \( V_{\text{object}} = 1 \, \text{l} = 0.001 \, \text{m}^3 \);
In Gasoline: \( F_B = 737 \times 0.001 \times 9.81 = 7.23 \, \text{N} \), \( W_{\text{immersed}} = 4.905 - 7.23 = -2.325 \, \text{N} \), in g: \( (-2.325 / 9.81) \times 1000 = -237.00 \, \text{g} \), in oz: \( (-2.325 / 9.81) \times 2.20462 \times 16 = -8.52 \, \text{oz} \), (Object will float);
In Mercury: \( F_B = 13560 \times 0.001 \times 9.81 = 133.00 \, \text{N} \), \( W_{\text{immersed}} = 4.905 - 133.00 = -128.095 \, \text{N} \), in g: \( (-128.095 / 9.81) \times 1000 = -13058.31 \, \text{g} \), in oz: \( (-128.095 / 9.81) \times 2.20462 \times 16 = -469.70 \, \text{oz} \), (Object will float).

5. Frequently Asked Questions (FAQ)

Q: What does a negative immersed weight mean?
A: A negative immersed weight indicates that the buoyant force exceeds the object's weight, causing it to float upwards. The negative value represents an upward force.

Q: Why does the immersed weight vary across fluids?
A: The immersed weight depends on the buoyant force, which varies with the fluid's density. Denser fluids (e.g., mercury) exert a greater buoyant force, reducing the immersed weight more than less dense fluids (e.g., gasoline).

Q: Can this calculator be used for partially submerged objects?
A: No, this calculator assumes the object is fully submerged. For partially submerged objects, the volume displaced would be less, and the buoyant force would need adjustment.