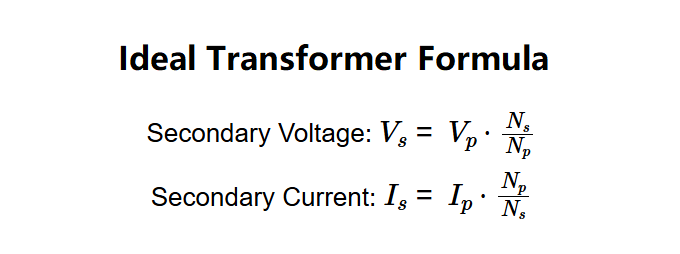Ideal Transformer Calculator

Calculation Type:

Primary Voltage (\( V_p \)):

Number of Primary Windings (\( N_p \)):

Number of Secondary Windings (\( N_s \)):

1. What is Ideal Transformer Calculator?

Definition: This calculator computes either the secondary voltage (\( V_s \)) or the secondary current (\( I_s \)) for an ideal transformer based on the primary voltage (\( V_p \)) or primary current (\( I_p \)), and the number of windings in the primary (\( N_p \)) and secondary (\( N_s \)) coils.

Purpose: It is used in electrical engineering to analyze and design ideal transformers, which are theoretical models that assume no losses, for applications like power distribution, voltage regulation, and impedance matching.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Secondary Voltage: \( V_s = V_p \cdot \frac{N_s}{N_p} \)
Secondary Current: \( I_s = I_p \cdot \frac{N_p}{N_s} \)

Where:

\( V_p \): Voltage at the primary coil (V)
\( V_s \): Voltage at the secondary coil (V)
\( I_p \): Current at the primary coil (A)
\( I_s \): Current at the secondary coil (A)
\( N_p \): Number of windings of the primary coil
\( N_s \): Number of windings of the secondary coil

Steps:

Select the calculation type: "Calculate Secondary Voltage" or "Calculate Secondary Current".
Enter the required parameters:
- For secondary voltage: Primary Voltage (\( V_p \)), Number of Primary Windings (\( N_p \)), and Number of Secondary Windings (\( N_s \)).
- For secondary current: Primary Current (\( I_p \)), Number of Primary Windings (\( N_p \)), and Number of Secondary Windings (\( N_s \)).
Convert all inputs to base units (V, A).
Calculate either the secondary voltage or secondary current based on the selected calculation type.
Convert the result to the selected output unit (V, mV, kV for voltage; A, mA, µA for current).
Display the result: if the value is less than 0.001 in the selected unit, use scientific notation; otherwise, display with 4 decimal places.

3. Importance of Ideal Transformer Calculation

Calculating the parameters of an ideal transformer is crucial for:

Voltage Transformation: Determining the secondary voltage to step up or step down the voltage for power distribution or device compatibility.
Current Transformation: Calculating the secondary current to match the load requirements while maintaining power conservation (since \( V_p \cdot I_p = V_s \cdot I_s \) in an ideal transformer).
Design and Analysis: Providing a theoretical baseline for transformer design, which can be adjusted for real-world losses in practical applications.

4. Using the Calculator

Example 1 (Calculate Secondary Voltage): Calculate the secondary voltage for an ideal transformer with \( V_p = 120 \, \text{V} \), \( N_p = 100 \), and \( N_s = 50 \):

Calculation Type: Calculate Secondary Voltage
Primary Voltage (\( V_p \)): 120 V
Number of Primary Windings (\( N_p \)): 100
Number of Secondary Windings (\( N_s \)): 50
Secondary Voltage (\( V_s \)): \( 120 \cdot \frac{50}{100} = 120 \cdot 0.5 = 60 \, \text{V} \)
Result: \( V_s = 60.0000 \, \text{V} \)

Example 2 (Calculate Secondary Current): Calculate the secondary current for an ideal transformer with \( I_p = 2 \, \text{A} \), \( N_p = 100 \), and \( N_s = 50 \):

Calculation Type: Calculate Secondary Current
Primary Current (\( I_p \)): 2 A
Number of Primary Windings (\( N_p \)): 100
Number of Secondary Windings (\( N_s \)): 50
Secondary Current (\( I_s \)): \( 2 \cdot \frac{100}{50} = 2 \cdot 2 = 4 \, \text{A} \)
Result: \( I_s = 4.0000 \, \text{A} \)

Example 3 (Demonstrating Scientific Notation for Voltage): Calculate the secondary voltage for an ideal transformer with \( V_p = 1 \, \text{mV} \), \( N_p = 1000 \), and \( N_s = 100000 \):

Calculation Type: Calculate Secondary Voltage
Primary Voltage (\( V_p \)): 1 mV = \( 1 \times 10^{-3} \) V
Number of Primary Windings (\( N_p \)): 1000
Number of Secondary Windings (\( N_s \)): 100000
Secondary Voltage (\( V_s \)): \( 1 \times 10^{-3} \cdot \frac{100000}{1000} = 1 \times 10^{-3} \cdot 100 = 0.1 \, \text{V} \), in mV: \( 0.1 \times 1000 = 100 \, \text{mV} \)
Result: \( V_s = 100.0000 \, \text{mV} \)

Example 4 (Demonstrating Scientific Notation for Current): Calculate the secondary current for an ideal transformer with \( I_p = 1 \, \text{mA} \), \( N_p = 1000 \), and \( N_s = 100000 \):

Calculation Type: Calculate Secondary Current
Primary Current (\( I_p \)): 1 mA = \( 1 \times 10^{-3} \) A
Number of Primary Windings (\( N_p \)): 1000
Number of Secondary Windings (\( N_s \)): 100000
Secondary Current (\( I_s \)): \( 1 \times 10^{-3} \cdot \frac{1000}{100000} = 1 \times 10^{-3} \cdot 0.01 = 1 \times 10^{-5} \, \text{A} \), in µA: \( 1 \times 10^{-5} \times 10^6 = 10 \, \text{µA} \)
Result: \( I_s = 10.0000 \, \text{µA} \)

5. Frequently Asked Questions (FAQ)

Q: What is an ideal transformer?
A: An ideal transformer is a theoretical model of a transformer that assumes no energy losses (e.g., no resistance in the windings, no leakage flux, and no core losses). It perfectly transfers electrical energy between the primary and secondary coils based on the turns ratio.

Q: Why is the turns ratio important?
A: The turns ratio (\( N_s / N_p \)) determines the voltage transformation between the primary and secondary coils. A higher \( N_s / N_p \) ratio steps up the voltage, while a lower ratio steps it down. The inverse ratio applies to current transformation.

Q: How does an ideal transformer conserve power?
A: In an ideal transformer, power is conserved, meaning \( V_p \cdot I_p = V_s \cdot I_s \). As the voltage increases (or decreases) based on the turns ratio, the current decreases (or increases) proportionally to maintain the same power.