1. What is Ideal Rocket Equation Calculator?

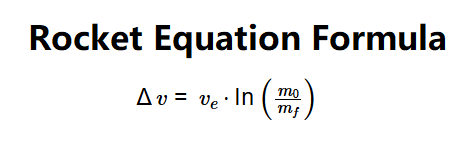
Definition: This calculator computes the change in velocity (\( \Delta v \)) of a rocket using the ideal rocket equation (Tsiolkovsky rocket equation), based on the effective exhaust velocity (\( v_e \)), initial mass (\( m_0 \)), and final mass (\( m_f \)).

Purpose: It is used in aerospace engineering to estimate the velocity change a rocket can achieve, which is critical for mission planning, such as reaching orbit or performing interplanetary travel.

2. How Does the Calculator Work?

The calculator uses the Tsiolkovsky rocket equation:

Formula:

• \( \Delta v = v_e \cdot \ln \left( \frac{m_0}{m_f} \right) \)

Where:

• \( \Delta v \): Change in velocity (m/s)
• \( v_e \): Effective exhaust velocity (m/s)
• \( m_0 \): Initial mass (rocket + propellant) (kg)
• \( m_f \): Final mass (rocket without propellant) (kg)

Unit Conversions:

• Effective Exhaust Velocity (\( v_e \)):
  • 1 m/s = 1 m/s
  • 1 km/s = 1000 m/s
  • 1 ft/s = 0.3048 m/s
• Mass (\( m_0 \), \( m_f \)):
  • 1 kg = 1 kg
  • 1 g = 0.001 kg
  • 1 ton = 1000 kg
  • 1 lb = 0.453592 kg
• Delta-V (\( \Delta v \)):
  • 1 m/s = 1 m/s
  • 1 km/s = 0.001 m/s
  • 1 ft/s = 3.28084 m/s

Steps:

• Enter the effective exhaust velocity (\( v_e \)), initial mass (\( m_0 \)), and final mass (\( m_f \)) with their respective units.
• Convert all inputs to base units (m/s for velocity, kg for mass).
• Calculate \( \Delta v \) using the Tsiolkovsky rocket equation.
• Convert the result to the selected unit for display.
• Display the result with 4 decimal places.

3. Importance of Delta-V Calculation

Calculating Delta-V is crucial for:

• Mission Planning: Determining the velocity changes required for orbital maneuvers, interplanetary travel, or landing.
• Rocket Design: Estimating the amount of propellant needed to achieve a desired velocity change.
• Space Exploration: Ensuring spacecraft can reach their destinations within the constraints of their propulsion systems.

4. Using the Calculator

Example: Calculate the Delta-V for a rocket with an effective exhaust velocity of \( v_e = 3000 \, \text{m/s} \), an initial mass of \( m_0 = 10000 \, \text{kg} \), and a final mass of \( m_f = 4000 \, \text{kg} \).

1. Enter \( v_e = 3000 \, \text{m/s} \), \( m_0 = 10000 \, \text{kg} \), and \( m_f = 4000 \, \text{kg} \).
2. The calculator computes:
   • \( \Delta v = 3000 \cdot \ln \left( \frac{10000}{4000} \right) \approx 3000 \cdot \ln(2.5) \approx 3000 \cdot 0.9163 \approx 2748.8736 \, \text{m/s} \).

5. Frequently Asked Questions (FAQ)

Q: What is Delta-V?
A: Delta-V (\( \Delta v \)) is the change in velocity a rocket can achieve, calculated using the Tsiolkovsky rocket equation, which depends on the effective exhaust velocity, initial mass, and final mass of the rocket.

Q: What is the Tsiolkovsky rocket equation?
A: The Tsiolkovsky rocket equation relates the change in velocity (\( \Delta v \)) to the effective exhaust velocity (\( v_e \)) and the mass ratio of the rocket, given by \( \Delta v = v_e \cdot \ln \left( \frac{m_0}{m_f} \right) \).

Q: How does the calculator handle different units?
A: The calculator allows users to input exhaust velocity in m/s, km/s, or ft/s, and masses in kg, g, ton, or lb. It converts all inputs to base units (m/s and kg) for calculation and displays the result in user-selected units (m/s, km/s, ft/s).

Ideal Rocket Equation Calculator© - All Rights Reserved 2025