Ideal Gas Volume Calculator

Number of Moles (\( n \)):

Temperature (\( T \)):

Pressure (\( P \)):

1. What is the Ideal Gas Volume Calculator?

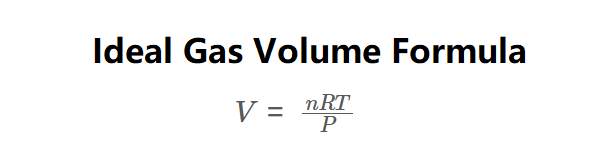
Definition: This calculator computes the volume (\( V \)) of an ideal gas based on the number of moles (\( n \)), temperature (\( T \)), and pressure (\( P \)).

Purpose: It is used in physics and chemistry to determine the volume occupied by a gas under ideal conditions, aiding in thermodynamic analysis and gas law applications.

2. How Does the Calculator Work?

The calculator uses the ideal gas law rearranged for volume:

\( V = \frac{nRT}{P} \)

Where:

\( V \): Volume (m³, L, cm³, ft³);
\( n \): Number of moles;
\( R \): Universal gas constant (\( 8.3145 \, \text{J·K}^{-1}\text{mol}^{-1} \));
\( T \): Temperature (K, °C, °F);
\( P \): Pressure (Pa, kPa, atm, bar).

Steps:

Enter the number of moles (\( n \)).
Enter the temperature (\( T \)) with its unit.
Enter the pressure (\( P \)) with its unit.
Convert temperature to Kelvin and pressure to Pa.
Calculate the volume using \( V = \frac{nRT}{P} \).
Convert the result to the selected output unit.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Ideal Gas Volume Calculation

Calculating the volume of an ideal gas is crucial for:

Chemistry: Understanding gas behavior in reactions.
Physics: Studying thermodynamic processes.
Engineering: Designing systems involving gases, like compressors or storage tanks.

4. Using the Calculator

Example 1: Calculate the volume with \( n = 1 \, \text{mol} \), \( T = 273.15 \, \text{K} \), \( P = 101325 \, \text{Pa} \):

Moles: \( n = 1 \, \text{mol} \);
Temperature: \( T = 273.15 \, \text{K} \);
Pressure: \( P = 101325 \, \text{Pa} \);
Volume: \( V = \frac{1 \times 8.3145 \times 273.15}{101325} \approx 0.0224 \, \text{m}^3 \);
Result (in L): \( V = 22.4000 \, \text{L} \).

Example 2: Calculate the volume with \( n = 0.5 \, \text{mol} \), \( T = 25 \, \text{°C} \), \( P = 1 \, \text{bar} \):

Moles: \( n = 0.5 \, \text{mol} \);
Temperature: \( T = 25 \, \text{°C} + 273.15 = 298.15 \, \text{K} \);
Pressure: \( P = 1 \, \text{bar} \times 100000 = 100000 \, \text{Pa} \);
Volume: \( V = \frac{0.5 \times 8.3145 \times 298.15}{100000} \approx 0.0124 \, \text{m}^3 \);
Result (in cm³): \( V = 12400.0000 \, \text{cm}^3 \).

5. Frequently Asked Questions (FAQ)

Q: What is the ideal gas law?
A: The ideal gas law (\( PV = nRT \)) relates pressure, volume, number of moles, and temperature for an ideal gas, assuming no intermolecular forces.

Q: Why must temperature be in Kelvin?
A: The ideal gas law requires absolute temperature in Kelvin for accurate calculations.

Q: Does this calculator apply to real gases?
A: This calculator uses the ideal gas law, which is an approximation. Real gases may deviate under high pressure or low temperature.