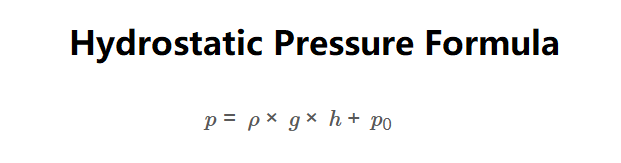Hydrostatic Pressure Calculator

Substance:

Density of the Fluid (\( \rho \)):

Gravitational Acceleration (\( g \)):

Depth (\( h \)):

External Pressure (\( p_0 \)):

1. What is Hydrostatic Pressure Calculator?

Definition: This calculator computes the hydrostatic pressure (\( p \)) exerted by a fluid at a given depth, based on the fluid's density (\( \rho \)), gravitational acceleration (\( g \)), depth (\( h \)), and external pressure (\( p_0 \)).

Purpose: It is used in physics and engineering to determine the pressure in a fluid at rest, such as in oceans, tanks, or dams, which is essential for designing structures and understanding fluid behavior.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula: \[ p = \rho \times g \times h + p_0 \] Where:

\( p \): Hydrostatic pressure (Pa, kPa, atm, psi)
\( \rho \): Density of the fluid (kg/m³, g/cm³, lb/ft³)
\( g \): Gravitational acceleration (m/s², ft/s²)
\( h \): Depth (m, km, cm, mm, ft, in, mi)
\( p_0 \): External pressure, usually atmospheric pressure (Pa, kPa, atm, psi)

Predefined Substances:

Ethanol: 785.1 kg/m³ (at 20°C)
Benzene: 873 kg/m³ (at 20°C)
Chloroform: 1465 kg/m³ (at 20°C)
Glycerine: 1259 kg/m³ (at 20°C)
Pure Water: 1000 kg/m³ (at 4°C, maximum density)
Seawater: 1022 kg/m³ (varies with salinity & temperature)
Mercury: 13590 kg/m³ (at 20°C)

Unit Conversions:

Density (\( \rho \)):
- 1 kg/m³ = 1 kg/m³
- 1 g/cm³ = 1000 kg/m³
- 1 lb/ft³ = 16.0185 kg/m³
Gravitational Acceleration (\( g \)):
- 1 m/s² = 1 m/s²
- 1 ft/s² = 0.3048 m/s²
Depth (\( h \)):
- 1 m = 1 m
- 1 km = 1000 m
- 1 cm = 0.01 m
- 1 mm = 0.001 m
- 1 ft = 0.3048 m
- 1 in = 0.0254 m
- 1 mi = 1609.34 m
External Pressure (\( p_0 \)):
- 1 Pa = 1 Pa
- 1 kPa = 1000 Pa
- 1 atm = 101325 Pa
- 1 psi = 6894.76 Pa
Hydrostatic Pressure (\( p \)):
- 1 Pa = 1 Pa
- 1 kPa = 1000 Pa
- 1 atm = 101325 Pa
- 1 psi = 6894.76 Pa

Steps:

Select a substance from the dropdown or choose "Custom" to enter your own density.
If a predefined substance is selected, the density field will auto-fill and become read-only.
Specify the density unit (kg/m³, g/cm³, lb/ft³).
Enter the gravitational acceleration (\( g \)) with its respective unit (m/s², ft/s²). Default is 9.80665 m/s² (Earth’s gravity).
Enter the depth (\( h \)) with its respective unit (m, km, cm, mm, ft, in, mi).
Enter the external pressure (\( p_0 \)) with its respective unit (Pa, kPa, atm, psi). Default is 101325 Pa (1 atm).
Select the desired unit for the pressure result (Pa, kPa, atm, psi).
Convert the density to kg/m³.
Convert the gravitational acceleration to m/s².
Convert the depth to meters.
Convert the external pressure to Pascals.
Calculate the hydrostatic pressure using \( p = \rho \times g \times h + p_0 \).
Convert the pressure to the selected unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Hydrostatic Pressure Calculation

Calculating hydrostatic pressure is crucial for:

Engineering Design: Ensuring structures like dams, submarines, and pipelines can withstand fluid pressure.
Oceanography: Understanding pressure at various depths in the ocean for marine biology and equipment design.
Hydrology: Analyzing groundwater pressure in wells and aquifers.

4. Using the Calculator

Examples:

Example 1: Calculate the hydrostatic pressure at a depth of 50 cm in pure water (select "Pure Water" from the dropdown, \( \rho = 1000 \, \text{kg/m³} \), \( g = 9.80665 \, \text{m/s²} \), \( p_0 = 101325 \, \text{Pa} \)), with pressure in Pascals:
- Select "Pure Water" (auto-fills \( \rho = 1000 \) kg/m³).
- Enter \( g = 9.80665 \) m/s².
- Enter \( h = 50 \) cm.
- Convert to m: \( h = 50 \times 0.01 = 0.5 \, \text{m} \)
- Enter \( p_0 = 101325 \) Pa.
- \( p = 1000 \times 9.80665 \times 0.5 + 101325 \)
- \( p = 4903.325 + 101325 = 106228.325 \) Pa
- Result: \( p = 106228.3250 \) Pa
Example 2: Calculate the hydrostatic pressure at a depth of 10 inches in mercury (select "Mercury" from the dropdown, \( \rho = 13590 \, \text{kg/m³} \), \( g = 9.80665 \, \text{m/s²} \), \( p_0 = 1 \, \text{atm} \)), with pressure in atmospheres:
- Select "Mercury" (auto-fills \( \rho = 13590 \) kg/m³).
- Enter \( g = 9.80665 \) m/s².
- Enter \( h = 10 \) in.
- Convert to m: \( h = 10 \times 0.0254 = 0.254 \, \text{m} \)
- Enter \( p_0 = 1 \) atm.
- Convert to Pa: \( p_0 = 1 \times 101325 = 101325 \, \text{Pa} \)
- \( p = 13590 \times 9.80665 \times 0.254 + 101325 \)
- \( p = 33848.3781 + 101325 = 135173.3781 \) Pa
- Convert to atm: \( p = 135173.3781 / 101325 \approx 1.3338 \) atm
- Result: \( p = 1.3338 \) atm

5. Frequently Asked Questions (FAQ)

Q: Why is gravitational acceleration set to 9.80665 m/s² by default?
A: This is the average gravitational acceleration on Earth’s surface, making it a standard value for most calculations.

Q: Can depth be negative?
A: No, depth represents the distance below the surface and must be zero or positive.

Q: What is the significance of external pressure (\( p_0 \))?
A: External pressure, often atmospheric pressure, is the pressure at the surface of the fluid, which adds to the pressure exerted by the fluid’s weight.

Q: Why do some densities vary, like seawater?
A: Seawater density depends on salinity and temperature, so the value provided (1022 kg/m³) is an average; actual values may differ based on conditions.