Hydrogen Energy Levels Calculator

1. What is the Hydrogen Energy Levels Calculator?

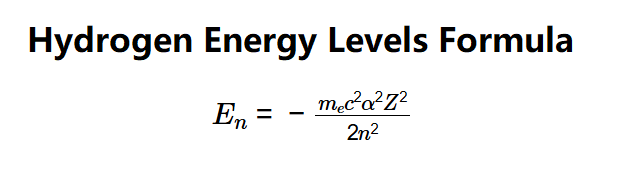
Definition: This calculator computes the energy (\( E_n \)) of an electron in a hydrogen-like atom at a specific energy level (\( n \)) for a given atomic number (\( Z \)).

Purpose: It is used in atomic physics to determine the quantized energy levels of electrons in hydrogen-like atoms, which is fundamental for understanding atomic spectra and quantum mechanics.

2. How Does the Calculator Work?

The calculator uses the following equation:

\( E_n = -\frac{m_e c^2 \alpha^2 Z^2}{2 n^2} \)

Where:

\( E_n \): Energy (J, neV, µeV, meV, eV, keV, MeV);
\( m_e \): Electron mass (\( 9.10938356 \times 10^{-31} \, \text{kg} \));
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \));
\( \alpha \): Fine structure constant (\( \frac{1}{137} \));
\( Z \): Atomic number;
\( n \): Energy level.

Steps:

Enter the energy level (\( n \)).
Enter the atomic number (\( Z \)).
Calculate the energy: \( E_n = -\frac{m_e c^2 \alpha^2 Z^2}{2 n^2} \).
Convert the energy to the selected output unit and display, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Hydrogen Energy Levels Calculation

Calculating the energy levels of hydrogen-like atoms is crucial for:

Atomic Physics: Understanding the quantized energy states of electrons.
Spectroscopy: Predicting the wavelengths of light emitted or absorbed during electron transitions.
Quantum Mechanics Education: Illustrating the application of quantum theory to atomic systems.

4. Using the Calculator

Example 1: Calculate the energy of an electron in a hydrogen atom (\( Z = 1 \)) at energy level \( n = 1 \):

Energy Level: \( n = 1 \);
Atomic Number: \( Z = 1 \);
Energy: \( E_1 = -\frac{9.10938356 \times 10^{-31} \times (299792458)^2 \times \left(\frac{1}{137}\right)^2 \times 1^2}{2 \times 1^2} \approx -2.179 \times 10^{-18} \, \text{J} \approx -13.606 \, \text{eV} \);
Result: \( E_1 = -13.6060 \, \text{eV} \).

Example 2 (Different \( Z \) and \( n \)): Calculate the energy for a helium ion (\( Z = 2 \)) at energy level \( n = 2 \):

Energy Level: \( n = 2 \);
Atomic Number: \( Z = 2 \);
Energy: \( E_2 = -\frac{9.10938356 \times 10^{-31} \times (299792458)^2 \times \left(\frac{1}{137}\right)^2 \times 2^2}{2 \times 2^2} \approx -8.716 \times 10^{-18} \, \text{J} \approx -54.423 \, \text{eV} \);
Result: \( E_2 = -54.4230 \, \text{eV} \).

5. Frequently Asked Questions (FAQ)

Q: What does a negative energy value mean?
A: The negative energy indicates that the electron is in a bound state, with energy measured relative to the ionized state (\( E = 0 \)) where the electron is free.

Q: Why does the energy depend on \( Z^2 \)?
A: The energy scales with \( Z^2 \) because the Coulomb attraction between the electron and nucleus increases with the nuclear charge (\( Z \)), making the energy levels more negative (more tightly bound) for higher \( Z \).

Q: Can this calculator be used for multi-electron atoms?
A: This calculator is designed for hydrogen-like atoms (one electron). For multi-electron atoms, electron-electron interactions complicate the energy levels, requiring more advanced models.