Hydraulic Gradient Calculator

Head at Point 1 (\( h_1 \)):

Head at Point 2 (\( h_2 \)):

Distance Between Points (\( l \)):

1. What is Hydraulic Gradient Calculator?

Definition: This calculator computes the hydraulic gradient (\( H_g \)) between two points in a flow system using the difference in hydraulic heads and the distance between the points.

Purpose: It is used in hydrogeology and fluid mechanics to determine the slope of the energy grade line, which drives groundwater flow and helps in analyzing seepage and aquifer behavior.

2. How Does the Calculator Work?

The calculator uses the hydraulic gradient equation:

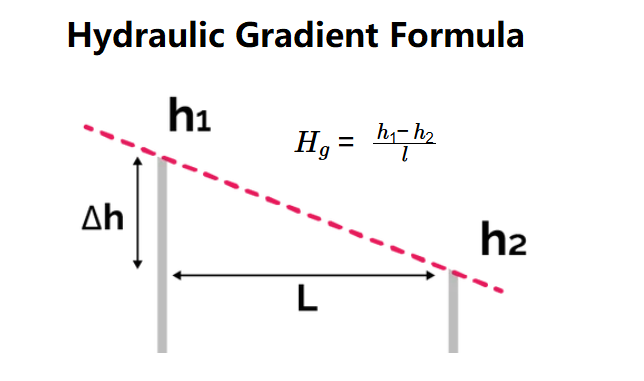
\( H_g = \frac{h_1 - h_2}{l} \)

Where:

\( H_g \): Hydraulic gradient (dimensionless);
\( h_1 \): Head at point 1 (m);
\( h_2 \): Head at point 2 (m);
\( l \): Distance between the two points (m).

Steps:

Enter the head at point 1 (\( h_1 \)) with its unit.
Enter the head at point 2 (\( h_2 \)) with its unit.
Enter the distance between the points (\( l \)) with its unit.
Convert \( h_1 \), \( h_2 \), and \( l \) to SI units (m).
Calculate the hydraulic gradient: \( H_g = \frac{h_1 - h_2}{l} \).
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 5 decimal places.

3. Importance of Hydraulic Gradient Calculation

Calculating the hydraulic gradient is crucial for:

Groundwater Flow: Determining the direction and rate of groundwater movement in aquifers.
Seepage Analysis: Assessing seepage through dams, levees, or soil layers in geotechnical engineering.
Pump Design: Estimating energy losses in flow systems to design efficient pumping systems.

4. Using the Calculator

Example 1 (SI Units): Calculate \( H_g \) between two points:

Head at Point 1: \( h_1 = 5 \, \text{m} \);
Head at Point 2: \( h_2 = 14 \, \text{m} \);
Distance Between Points: \( l = 9 \, \text{m} \);
Hydraulic Gradient: \( H_g = \frac{h_1 - h_2}{l} = \frac{5 - 14}{9} = -1 \);
Result: \( H_g = -1.00000 \).

Example 2 (Mixed Units): Calculate \( H_g \) between two points:

Head at Point 1: \( h_1 = 20 \, \text{ft} \);
Convert \( h_1 \): \( h_1 = 20 \times 0.3048 = 6.096 \, \text{m} \);
Head at Point 2: \( h_2 = 15 \, \text{ft} \);
Convert \( h_2 \): \( h_2 = 15 \times 0.3048 = 4.572 \, \text{m} \);
Distance Between Points: \( l = 1000 \, \text{cm} \);
Convert \( l \): \( l = 1000 / 100 = 10 \, \text{m} \);
Hydraulic Gradient: \( H_g = \frac{h_1 - h_2}{l} = \frac{6.096 - 4.572}{10} = 0.1524 \);
Result: \( H_g = 0.15240 \).

5. Frequently Asked Questions (FAQ)

Q: What does a negative hydraulic gradient mean?
A: A negative hydraulic gradient, like \(-1 \, \text{m/m}\), indicates that the hydraulic head decreases along the flow path (e.g., from point 1 to point 2), meaning water flows downward in that direction.

Q: Why is the hydraulic gradient dimensionless?
A: The hydraulic gradient is the ratio of the change in head (in meters) to the distance (in meters), so the units cancel out, making it a dimensionless quantity.

Q: Can this calculator be used for vertical flow?
A: Yes, the calculator works for both horizontal and vertical flow, as long as the heads and distance are measured along the flow path.