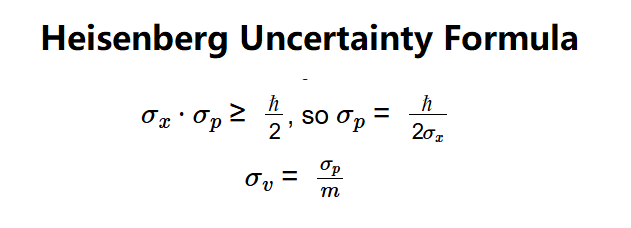Heisenberg Uncertainty Calculator

Position Uncertainty (\( \sigma_x \)):

Object Mass (\( m \)):

Momentum Uncertainty (\( \sigma_p \)):

kg·m/s

Velocity Uncertainty (\( \sigma_v \)):

1. What is the Heisenberg Uncertainty Calculator?

Definition: This calculator uses the Heisenberg uncertainty principle to compute the minimum momentum uncertainty (\( \sigma_p \)) and velocity uncertainty (\( \sigma_v \)) of an object given its position uncertainty (\( \sigma_x \)) and mass (\( m \)).

Purpose: It is used in quantum mechanics to quantify the fundamental limit on the precision with which position and momentum (or velocity) can be simultaneously known.

2. How Does the Calculator Work?

The calculator uses the following equations:

\( \sigma_x \cdot \sigma_p \geq \frac{\hbar}{2} \), so \( \sigma_p = \frac{\hbar}{2 \sigma_x} \)
\( \sigma_v = \frac{\sigma_p}{m} \)

Where:

\( \sigma_x \): Position uncertainty (m, cm, mm, nm, pm, Å);
\( \sigma_p \): Momentum uncertainty (kg·m/s);
\( \sigma_v \): Velocity uncertainty (m/s, km/s, cm/s, mm/s, km/h, ft/s, mph, mi/s, c);
\( m \): Mass of the object (various units);
\( \hbar \): Reduced Planck constant (\( 1.054571817 \times 10^{-34} \, \text{J·s} \)).

Steps:

Enter the position uncertainty (\( \sigma_x \)) with its unit.
Enter the mass of the object (\( m \)) with its unit.
Convert the inputs to base units (meters for \( \sigma_x \), kg for \( m \)).
Calculate the momentum uncertainty: \( \sigma_p = \frac{\hbar}{2 \sigma_x} \).
Calculate the velocity uncertainty: \( \sigma_v = \frac{\sigma_p}{m} \).
Convert the velocity uncertainty to the selected output unit and display both \( \sigma_p \) and \( \sigma_v \), formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Heisenberg Uncertainty Calculation

Calculating the Heisenberg uncertainty is crucial for:

Quantum Mechanics: Understanding the fundamental limits of measurement at the quantum scale.
Particle Physics: Analyzing the behavior of particles like electrons and protons.
Quantum Technologies: Designing systems like quantum computers that operate within these uncertainty constraints.

4. Using the Calculator

Example 1: Calculate the uncertainties for an electron with a position uncertainty of 5.8 nm:

Position Uncertainty: \( \sigma_x = 5.8 \, \text{nm} = 5.8 \times 10^{-9} \, \text{m} \);
Mass: \( m = 1 \, m_e = 9.10938356 \times 10^{-31} \, \text{kg} \);
Momentum Uncertainty: \( \sigma_p = \frac{1.054571817 \times 10^{-34}}{2 \times 5.8 \times 10^{-9}} \approx 9.100 \times 10^{-27} \, \text{kg·m/s} \);
Velocity Uncertainty: \( \sigma_v = \frac{9.100 \times 10^{-27}}{9.10938356 \times 10^{-31}} \approx 9.990 \times 10^3 \, \text{m/s} \);
Result: \( \sigma_p = 9.1000 \times 10^{-27} \, \text{kg·m/s} \), \( \sigma_v = 9.9900 \times 10^3 \, \text{m/s} \).

Example 2 (Different Mass and Unit): Calculate the uncertainties for a proton with a position uncertainty of 1 pm:

Position Uncertainty: \( \sigma_x = 1 \, \text{pm} = 1 \times 10^{-12} \, \text{m} \);
Mass: \( m = 1 \, m_p = 1.6726219 \times 10^{-27} \, \text{kg} \);
Momentum Uncertainty: \( \sigma_p = \frac{1.054571817 \times 10^{-34}}{2 \times 1 \times 10^{-12}} \approx 5.273 \times 10^{-23} \, \text{kg·m/s} \);
Velocity Uncertainty: \( \sigma_v = \frac{5.273 \times 10^{-23}}{1.6726219 \times 10^{-27}} \approx 3.153 \times 10^4 \, \text{m/s} \approx 1.052 \times 10^{-4} \, \text{c} \);
Result: \( \sigma_p = 5.2730 \times 10^{-23} \, \text{kg·m/s} \), \( \sigma_v = 1.0520 \times 10^{-4} \, \text{c} \).

5. Frequently Asked Questions (FAQ)

Q: What does the Heisenberg uncertainty principle tell us?
A: It states that the position and momentum of a particle cannot be measured simultaneously with arbitrary precision; the product of their uncertainties must be at least \( \frac{\hbar}{2} \).

Q: Why does a smaller position uncertainty increase the momentum uncertainty?
A: The Heisenberg principle requires \( \sigma_x \cdot \sigma_p \geq \frac{\hbar}{2} \). A smaller \( \sigma_x \) forces \( \sigma_p \) to be larger to satisfy the inequality.

Q: Is this calculator applicable for macroscopic objects?
A: The uncertainty principle applies to all objects, but for macroscopic objects (e.g., a car), the uncertainties are so small that they are negligible in classical physics.