1. What is Heat Transfer Calculator?

Definition: This calculator computes the heat transferred (\( Q \)) in a system using three types of heat transfer equations: sensible heat, conduction, and radiation.

Purpose: It is used in physics and engineering to determine the amount of heat energy transferred, aiding in the design of thermal systems, insulation, and energy management.

2. How Does the Calculator Work?

The calculator supports three heat transfer methods:

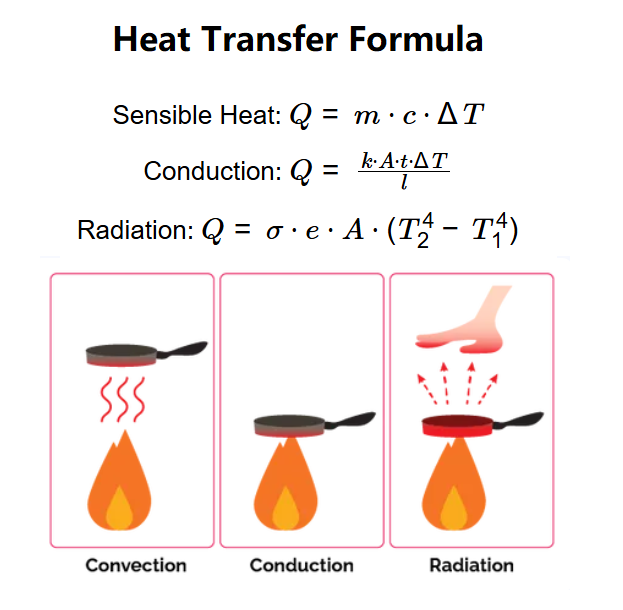
• Sensible Heat: \( Q = m \cdot c \cdot \Delta T \)
• Conduction: \( Q = \frac{k \cdot A \cdot t \cdot \Delta T}{l} \)
• Radiation: \( Q = \sigma \cdot e \cdot A \cdot (T_2^4 - T_1^4) \)

Where:

• \( Q \): Heat transferred (J);
• \( m \): Mass (kg);
• \( c \): Specific heat (J/(kg·°C));
• \( \Delta T \): Temperature difference (°C or K);
• \( k \): Thermal conductivity (W/(m·°C));
• \( A \): Surface area (m²);
• \( t \): Time (s);
• \( l \): Thickness (m);
• \( \sigma \): Stefan-Boltzmann constant (\( 5.67 \times 10^{-8} \, \text{J/(s·m}^2\text{·K}^4\text{)} \));
• \( e \): Emissivity (dimensionless);
• \( T_1, T_2 \): Temperatures (K).

Steps:

• Select the calculation mode (sensible heat, conduction, or radiation).
• Enter the required parameters based on the selected mode, including appropriate units.
• Convert all inputs to base units (kg for mass, J/(kg·°C) for specific heat, W/(m·°C) for thermal conductivity, m² for area, s for time, m for thickness, °C or K for temperature differences, K for absolute temperatures).
• Calculate the heat transferred \( Q \) based on the selected mode.
• Convert the result to the selected output unit (J, kJ, MJ, Wh, kWh, ft-lb, kcal, or eV).
• Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Heat Transfer Calculation

Calculating heat transfer is crucial for:

• Thermal Management: Designing systems to efficiently transfer or retain heat, such as in HVAC or electronics cooling.
• Material Selection: Choosing materials with appropriate thermal properties for insulation or conduction.
• Energy Efficiency: Optimizing energy use in processes involving heat exchange.

4. Using the Calculator

Example 1 (Sensible Heat Mode): Calculate the heat transferred for heating water:

• Mass: \( m = 1 \, \text{kg} \);
• Specific Heat: \( c = 4186 \, \text{J/(kg·K)} \) (Water);
• Temperature Difference: \( \Delta T = 10 \, \text{K} \);
• Heat Transferred: \( Q = 1 \times 4186 \times 10 = 41860 \, \text{J} \);
• Result in kJ: \( Q = 41860 / 1000 = 41.8600 \, \text{kJ} \);
• Result in kcal: \( Q = 41860 / 4184 \approx 10.0048 \, \text{kcal} \).

Example 2 (Conduction Mode): Calculate the heat transferred through a copper wall:

• Thermal Conductivity: \( k = 401 \, \text{W/(m·°C)} \) (Copper);
• Surface Area: \( A = 1 \, \text{m}^2 \);
• Time: \( t = 1 \, \text{h} = 3600 \, \text{s} \);
• Temperature Difference: \( \Delta T = 20 \, \text{°C} \);
• Thickness: \( l = 1 \, \text{cm} = 0.01 \, \text{m} \);
• Heat Transferred: \( Q = \frac{401 \times 1 \times 3600 \times 20}{0.01} = 288720000 \, \text{J} \);
• Result in MJ: \( Q = 288720000 / 1000000 = 288.7200 \, \text{MJ} \);
• Result in kWh: \( Q = 288720000 / 3600000 \approx 80.2000 \, \text{kWh} \).

5. Frequently Asked Questions (FAQ)

Q: What does a negative \( Q \) indicate?
A: A negative \( Q \) means heat is lost from the system to the surroundings.

Q: Why do temperatures need to be in Kelvin for radiation?
A: The Stefan-Boltzmann law requires absolute temperatures (Kelvin) because it involves \( T^4 \), and negative temperatures would cause errors.

Q: Can this calculator handle combined heat transfer types?
A: No, this calculator handles one type at a time. For combined effects, calculate each type separately and sum the results.

Heat Transfer Calculator© - All Rights Reserved 2025