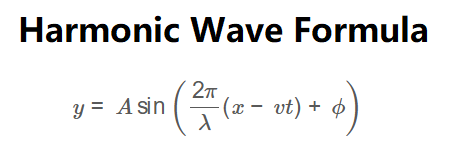Harmonic Wave Equation Calculator

Position (\( x \)):

Time (\( t \)):

Wave Velocity (\( v \)):

Wavelength (\( \lambda \)):

Amplitude (\( A \)):

Initial Phase (\( \phi \)):

Result

Displacement (\( y \)):

1. What is a Harmonic Wave Equation Calculator?

Definition: This calculator computes the displacement (\( y \)) of a point along a harmonic wave at a given position (\( x \)) and time (\( t \)), based on the wave’s properties.

Purpose: It is used in physics to analyze the behavior of harmonic waves, such as sound waves, light waves, or mechanical waves, by determining the displacement at specific points and times.

2. How Does the Calculator Work?

The calculator uses the following formula:

Displacement: \[ y = A \sin \left( \frac{2\pi}{\lambda} (x - vt) + \phi \right) \] Where:

\( y \): Displacement (mm, cm, m, in, ft, yd)
\( x \): Position (mm, cm, m, in, ft, yd)
\( t \): Time (sec, min, hr)
\( v \): Wave velocity (m/s, km/h, ft/s, mph, km/s, mi/s)
\( \lambda \): Wavelength (mm, cm, m, in, ft, yd)
\( A \): Amplitude (mm, cm, m, in, ft, yd)
\( \phi \): Initial phase (radians, degrees)

Unit Conversions:

Position (\( x \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
Time (\( t \)): sec, min (1 min = 60 sec), hr (1 hr = 3600 sec)
Wave Velocity (\( v \)): m/s, km/h (1 km/h = \( \frac{1000}{3600} \) m/s ≈ 0.277777778 m/s), ft/s (1 ft/s = 0.3048 m/s), mph (1 mph = 0.44704 m/s), km/s (1 km/s = 1000 m/s), mi/s (1 mi/s = 1609.344 m/s)
Wavelength (\( \lambda \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
Amplitude (\( A \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
Initial Phase (\( \phi \)): radians, degrees (1 degree = \( \frac{\pi}{180} \) radians)
Displacement (\( y \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)

Steps:

Enter the position, time, wave velocity, wavelength, amplitude, and initial phase, and select their units.
Convert all inputs to base units (m for distances, sec for time, m/s for velocity, radians for phase).
Calculate the displacement using the harmonic wave equation.
Convert the displacement to the selected unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 3 decimal places.

3. Importance of Harmonic Wave Equation Calculation

Calculating the displacement of a harmonic wave is crucial for:

Physics Education: Understanding the behavior of waves and their properties.
Engineering Applications: Analyzing wave propagation in systems like acoustics, optics, or mechanical vibrations.
Wave Analysis: Determining the position of points along a wave at specific times for simulations or experiments.

4. Using the Calculator

Examples:

Example 1: For \( x = 2 \, \text{m} \), \( t = 1 \, \text{sec} \), \( v = 5 \, \text{m/s} \), \( \lambda = 4 \, \text{m} \), \( A = 0.1 \, \text{m} \), \( \phi = 0 \, \text{radians} \), displacement in m:
- Displacement: \( y = 0.1 \sin \left( \frac{2\pi}{4} (2 - 5 \times 1) + 0 \right) = 0.1 \sin \left( \frac{\pi}{2} \times (-3) \right) = 0.1 \sin \left( -\frac{3\pi}{2} \right) = 0.1 \times 1 = 0.100 \, \text{m} \)
Example 2: For \( x = 10 \, \text{cm} \), \( t = 2 \, \text{min} \), \( v = 10 \, \text{km/h} \), \( \lambda = 50 \, \text{cm} \), \( A = 5 \, \text{cm} \), \( \phi = 90 \, \text{degrees} \), displacement in cm:
- Convert: \( x = 10 \times 0.01 = 0.1 \, \text{m} \), \( t = 2 \times 60 = 120 \, \text{sec} \), \( v = 10 \times \frac{1000}{3600} = 2.77778 \, \text{m/s} \), \( \lambda = 50 \times 0.01 = 0.5 \, \text{m} \), \( A = 5 \times 0.01 = 0.05 \, \text{m} \), \( \phi = 90 \times \frac{\pi}{180} = \frac{\pi}{2} \, \text{radians} \)
- Displacement: \( y = 0.05 \sin \left( \frac{2\pi}{0.5} (0.1 - 2.77778 \times 120) + \frac{\pi}{2} \right) = 0.05 \sin \left( 4\pi (0.1 - 333.3336) + \frac{\pi}{2} \right) = 0.05 \sin \left( -4180.5 + \frac{\pi}{2} \right) \approx 0.05 \sin \left( -4180.5 + 1.5708 \right) \approx 0.05 \times (-0.999) = -0.04995 \, \text{m} \), \( y = -0.04995 \times 100 = -4.995 \, \text{cm} \)

5. Frequently Asked Questions (FAQ)

Q: What is a harmonic wave?
A: A harmonic wave is a wave that follows a sinusoidal pattern, characterized by its amplitude, wavelength, velocity, and phase, often used to model phenomena like sound or light waves.

Q: What does the initial phase (\(\phi\)) represent?
A: The initial phase (\(\phi\)) determines the starting point of the wave’s oscillation at \( x = 0 \) and \( t = 0 \), shifting the wave along the horizontal axis.

Q: How does the wave velocity affect the displacement?
A: The wave velocity (\( v \)) determines how fast the wave propagates, affecting the position of the wave crest at a given time, which in turn influences the displacement at a specific point.