Hair Diffraction Calculator

$Hair Diffraction Formula$

Position of Dark Point ($ n $):

Wavelength ($ \lambda $):

Distance from Hair to Screen ($ D $):

Distance to Dark Spot ($ x $):

1. What is the Hair Diffraction Calculator?

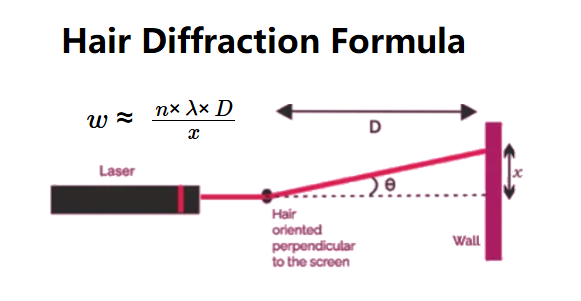
Definition: This calculator uses the diffraction formula for a single slit (approximated by a hair) to compute the width of the hair ($ w $) and the diffraction angle ($ \theta $) based on the position of the dark point ($ n $), the wavelength of the light ($ \lambda $), the distance from the hair to the screen ($ D $), and the distance from the center of the diffraction pattern to the dark spot ($ x $).

Purpose: It is used in optics to estimate the width of a thin object (like a hair) by observing its diffraction pattern, demonstrating the wave nature of light and the principles of single-slit diffraction.

2. How Does the Calculator Work?

The calculator uses the following equations:

$ w \approx \frac{n \times \lambda \times D}{x} $
$ \theta \approx \frac{x}{D} \quad (\text{small-angle approximation, in radians}) $

Where:

$ n $: Position of the dark point (integer, typically $ n = 1 $);
$ \lambda $: Wavelength of light (m, nm, pm, µm, Å, in, ft, yard, converted to m);
$ D $: Distance from hair to screen (m, cm, mm, in, ft, yard, converted to m);
$ x $: Distance from the center of the diffraction pattern to the dark spot (m, cm, mm, in, ft, yard, converted to m);
$ w $: Width of the hair (m, µm, mm);
$ \theta $: Diffraction angle (degrees or radians).

Steps:

Enter the position of the dark point ($ n $).
Enter the wavelength ($ \lambda $) with its unit.
Enter the distance from the hair to the screen ($ D $) with its unit.
Enter the distance from the center of the diffraction pattern to the dark spot ($ x $) with its unit.
Convert the wavelength, distance $ D $, and distance $ x $ to meters.
Calculate the hair width: $ w \approx \frac{n \times \lambda \times D}{x} $.
Calculate the diffraction angle: $ \theta \approx \frac{x}{D} $ (in radians).
Convert the angle to degrees if selected, and the hair width to the chosen output unit.
Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Hair Diffraction Calculation

Calculating the hair width and diffraction angle is important for:

Optics Education: Demonstrating the principles of single-slit diffraction and the wave nature of light using a simple experiment.
Experimental Physics: Measuring the dimensions of thin objects (like hairs or wires) using diffraction patterns.
Interdisciplinary Applications: Understanding diffraction in biological systems (e.g., hair or fibers) and optical instruments.

4. Using the Calculator

Example 1: Calculate the hair width and diffraction angle using a red laser with the new units:

Position of Dark Point: $ n = 1 $;
Wavelength: $ \lambda = 650 \, \text{nm} = 6.5 \times 10^{-7} \, \text{m} $;
Distance from Hair to Screen: $ D = 1 \, \text{yard} = 0.9144 \, \text{m} $;
Distance to Dark Spot: $ x = 1 \, \text{in} = 0.0254 \, \text{m} $;
Hair Width: $ w \approx \frac{1 \times 6.5 \times 10^{-7} \times 0.9144}{0.0254} \approx 2.34 \times 10^{-5} \, \text{m} = 23.4 \, \text{µm} $;
Diffraction Angle: $ \theta \approx \frac{0.0254}{0.9144} \approx 0.0278 \, \text{rad} \approx 1.591 \, \text{°} $;
Result: $ w = 23.4000 \, \text{µm} $, $ \theta = 1.5910 \, \text{°} $.

Example 2: Calculate the hair width and diffraction angle using a green laser with the new units:

Position of Dark Point: $ n = 1 $;
Wavelength: $ \lambda = 532 \, \text{pm} = 5.32 \times 10^{-10} \, \text{m} $;
Distance from Hair to Screen: $ D = 2 \, \text{ft} = 0.6096 \, \text{m} $;
Distance to Dark Spot: $ x = 5 \, \text{mm} = 0.005 \, \text{m} $;
Hair Width: $ w \approx \frac{1 \times 5.32 \times 10^{-10} \times 0.6096}{0.005} \approx 6.484 \times 10^{-8} \, \text{m} = 0.0648 \, \text{µm} $;
Diffraction Angle: $ \theta \approx \frac{0.005}{0.6096} \approx 0.0082 \, \text{rad} \approx 0.470 \, \text{°} $;
Result: $ w = 0.0648 \, \text{µm} $, $ \theta = 0.4700 \, \text{°} $.

5. Frequently Asked Questions (FAQ)

Q: What does the hair diffraction calculation tell us?
A: It allows us to estimate the width of a thin object (like a hair) by observing the diffraction pattern it creates when light passes through it, and it provides the angle at which the dark fringe appears, illustrating the wave nature of light.

Q: Why is the small-angle approximation used?
A: The distance from the hair to the screen ($ D $) is typically much larger than the distance to the dark spot ($ x $), making the diffraction angle ($ \theta $) very small. For small angles, $ \sin(\theta) \approx \theta $, simplifying the calculation.

Q: Can this calculator be used for objects other than hair?
A: Yes, it can be used for any thin object (e.g., a wire or slit) that acts as a single slit for diffraction, as long as the diffraction pattern is observable and the small-angle approximation holds.