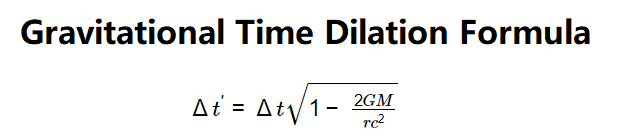Gravitational Time Dilation Calculator

Time Interval Uninfluenced by Gravity (\( \Delta t \)):

Mass of Object (\( M \)):

Distance from Center (\( r \)):

Time Interval Affected by Gravity (\( \Delta t' \)):

1. What is Gravitational Time Dilation Calculator?

Definition: This calculator computes the time interval (\( \Delta t' \)) affected by gravity near a massive object, based on the time interval (\( \Delta t \)) uninfluenced by gravity, the mass (\( M \)) of the object, and the distance (\( r \)) from its center.

Purpose: It is used in general relativity to understand how time passes differently in regions of varying gravitational strength, a phenomenon predicted by Einstein's theory of general relativity.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula:

\( \Delta t' = \Delta t \sqrt{1 - \frac{2 G M}{r c^2}} \)

Where:

\( \Delta t' \): Time interval affected by gravity (ps, ns, μs, ms, s, min, hr, day, wk, mo, yr, myr, byr, univ)
\( \Delta t \): Time interval uninfluenced by gravity (ps, ns, μs, ms, s, min, hr, day, wk, mo, yr, myr, byr, univ)
\( M \): Mass of the object (kg, t, oz, lb, st, us_ton, long_ton, earth_mass, solar_mass)
\( G \): Gravitational constant (\( 6.6743 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2 \))
\( r \): Distance from the center of the object (m, km, ft, yd, mi, nmi, earth_radius, solar_radius, ly, au, pc, Mly, Mpc)
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \))

Unit Conversions:

Time (\( \Delta t \), \( \Delta t' \)):
- 1 ps = \( 10^{-12} \) s
- 1 ns = \( 10^{-9} \) s
- 1 μs = \( 10^{-6} \) s
- 1 ms = \( 10^{-3} \) s
- 1 s = 1 s
- 1 min = 60 s
- 1 hr = 3600 s
- 1 day = 86400 s
- 1 wk = 604800 s
- 1 mo = 2.628e6 s
- 1 yr = 3.156e7 s
- 1 myr = 3.156e13 s
- 1 byr = 3.156e16 s
- 1 univ = 1.38e10 yr = \( 1.38 \times 10^{10} \times 3.156 \times 10^7 \) s
Mass (\( M \)):
- 1 kg = 1 kg
- 1 t = 1000 kg
- 1 oz = 0.0283495 kg
- 1 lb = 0.453592 kg
- 1 st = 6.35029 kg
- 1 us_ton = 907.185 kg
- 1 long_ton = 1016.05 kg
- 1 earth_mass = \( 5.972 \times 10^{24} \) kg
- 1 solar_mass = \( 1.989 \times 10^{30} \) kg
Distance (\( r \)):
- 1 m = 1 m
- 1 km = 1000 m
- 1 ft = 0.3048 m
- 1 yd = 0.9144 m
- 1 mi = 1609.344 m
- 1 nmi = 1852 m
- 1 earth_radius = \( 6.371 \times 10^6 \) m
- 1 solar_radius = \( 6.957 \times 10^8 \) m
- 1 ly = \( 9.4607304725808 \times 10^{15} \) m
- 1 au = \( 1.496 \times 10^{11} \) m
- 1 pc = \( 3.08568 \times 10^{16} \) m
- 1 Mly = \( 9.4607304725808 \times 10^{21} \) m
- 1 Mpc = \( 3.08568 \times 10^{22} \) m

Steps:

Enter the time interval uninfluenced by gravity (\( \Delta t \)) with its respective unit (ps, ns, μs, ms, s, min, hr, day, wk, mo, yr, myr, byr, univ).
Enter the mass of the object (\( M \)) with its respective unit (kg, t, oz, lb, st, us_ton, long_ton, earth_mass, solar_mass).
Enter the distance from the center of the object (\( r \)) with its respective unit (m, km, ft, yd, mi, nmi, earth_radius, solar_radius, ly, au, pc, Mly, Mpc).
Convert the time interval to seconds, mass to kilograms, and distance to meters.
Calculate the time interval affected by gravity using \( \Delta t' = \Delta t \sqrt{1 - \frac{2 G M}{r c^2}} \).
Select the desired unit for the result (ps, ns, μs, ms, s, min, hr, day, wk, mo, yr, myr, byr, univ).
Convert the result to the selected unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Gravitational Time Dilation Calculation

Calculating gravitational time dilation is crucial for:

General Relativity: It demonstrates how gravity affects the passage of time, a key prediction of Einstein's theory of general relativity.
GPS Technology: Gravitational time dilation must be accounted for in GPS satellites, which experience weaker gravity than on Earth's surface, causing their clocks to tick faster.
Astrophysics: It helps understand time differences near massive objects like black holes, where gravitational effects are extreme.

4. Using the Calculator

Examples:

Example 1: Calculate the time dilation for a time interval of 1 second near the Sun (\( M = 1 \, \text{solar mass} \)) at a distance of 1 AU, with the result in seconds:
- Enter \( \Delta t = 1 \) s.
- Enter \( M = 1 \) solar mass.
- Convert mass: \( M = 1 \times 1.989 \times 10^{30} = 1.989 \times 10^{30} \) kg.
- Enter \( r = 1 \) AU.
- Convert distance: \( r = 1 \times 1.496 \times 10^{11} = 1.496 \times 10^{11} \) m.
- \( \frac{2 G M}{r c^2} = \frac{2 \times 6.6743 \times 10^{-11} \times 1.989 \times 10^{30}}{1.496 \times 10^{11} \times (299,792,458)^2} \approx 1.975 \times 10^{-8} \)
- \( \Delta t' = 1 \times \sqrt{1 - 1.975 \times 10^{-8}} \approx 0.9999999901 \) s
- Result: \( \Delta t' = 1.0000 \) s
Example 2: Calculate the time dilation for a time interval of 1 hour near the Earth (\( M = 1 \, \text{Earth mass} \)) at a distance of 1 Earth radius, with the result in milliseconds:
- Enter \( \Delta t = 1 \) hr.
- Convert time: \( \Delta t = 1 \times 3600 = 3600 \) s.
- Enter \( M = 1 \) Earth mass.
- Convert mass: \( M = 1 \times 5.972 \times 10^{24} = 5.972 \times 10^{24} \) kg.
- Enter \( r = 1 \) Earth radius.
- Convert distance: \( r = 1 \times 6.371 \times 10^6 = 6.371 \times 10^6 \) m.
- \( \frac{2 G M}{r c^2} = \frac{2 \times 6.6743 \times 10^{-11} \times 5.972 \times 10^{24}}{6.371 \times 10^6 \times (299,792,458)^2} \approx 1.39 \times 10^{-9} \)
- \( \Delta t' = 3600 \times \sqrt{1 - 1.39 \times 10^{-9}} \approx 3599.9999975 \) s
- Convert to ms: \( \Delta t' = 3599.9999975 \times 1000 = 3,599,999.9975 \) ms
- Result: \( \Delta t' = 3600000.0000 \) ms

5. Frequently Asked Questions (FAQ)

Q: What is gravitational time dilation?
A: Gravitational time dilation is the phenomenon where time passes more slowly in stronger gravitational fields, as predicted by Einstein's theory of general relativity.

Q: Why does time slow down near massive objects?
A: According to general relativity, gravity warps spacetime, and clocks in stronger gravitational fields tick more slowly compared to those in weaker fields or at infinite distance.

Q: What is the Schwarzschild radius, and why does it matter?
A: The Schwarzschild radius is the radius at which the term \( \frac{2 G M}{r c^2} = 1 \), marking the event horizon of a black hole. The formula is not valid inside this radius, as it would imply imaginary time dilation.