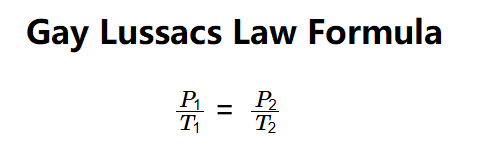Gay-Lussac's Law Calculator

Initial Conditions

Initial Pressure (\( P_1 \)):

Initial Temperature (\( T_1 \)):

Final Conditions (Leave one field blank to solve for it)

Final Pressure (\( P_2 \)):

Final Temperature (\( T_2 \)):

1. What is Gay-Lussac's Law Calculator?

Definition: This calculator computes the pressure or temperature of an ideal gas during an isochoric (constant-volume) process using Gay-Lussac's Law, which states that the pressure of a gas is directly proportional to its absolute temperature when volume and mass are constant.

Purpose: It is used in thermodynamics and physics to analyze how changes in temperature affect the pressure of a gas (or vice versa) in a rigid container, such as in pressure cookers, aerosol cans, or vehicle tires.

2. How Does the Calculator Work?

The calculator uses the following formula:

\( \frac{P_1}{T_1} = \frac{P_2}{T_2} \)

Where:

\( P_1 \): Initial pressure;
\( T_1 \): Initial temperature (in Kelvin);
\( P_2 \): Final pressure;
\( T_2 \): Final temperature (in Kelvin).

Steps:

Enter the initial pressure (\( P_1 \)) and temperature (\( T_1 \)) with their units.
Enter either the final pressure (\( P_2 \)) or final temperature (\( T_2 \)) with its unit, leaving the other field blank to solve for it.
Convert all inputs to base units (Pa for pressure, K for temperature).
Calculate the unknown variable using the formula: \( P_2 = P_1 \times \frac{T_2}{T_1} \) (if solving for \( P_2 \)) or \( T_2 = T_1 \times \frac{P_2}{P_1} \) (if solving for \( T_2 \)).
Convert the result back to the selected unit and display it, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 5 decimal places.

3. Importance of Gay-Lussac's Law Calculation

Calculating pressure or temperature changes using Gay-Lussac's Law is crucial for:

Safety in Pressurized Systems: Understanding pressure changes in containers like aerosol cans or pressure cookers to prevent explosions due to overheating.
Automotive Applications: Monitoring tire pressure changes with temperature variations to ensure safe driving conditions.
Industrial Processes: Managing gas behavior in sealed systems during heating or cooling processes, such as in chemical reactors or HVAC systems.

4. Using the Calculator

Example 1 (Solving for Final Pressure): Calculate \( P_2 \) for a gas in a rigid container with the following properties:

Initial Pressure: \( P_1 = 100 \, \text{kPa} \);
Initial Temperature: \( T_1 = 20 \, \text{°C} \);
Final Temperature: \( T_2 = 400 \, \text{°C} \);
Convert temperatures to Kelvin: \( T_1 = 20 + 273.15 = 293.15 \, \text{K} \), \( T_2 = 400 + 273.15 = 673.15 \, \text{K} \);
Convert pressure to Pa: \( P_1 = 100 \times 1000 = 100000 \, \text{Pa} \);
Final Pressure: \( P_2 = P_1 \times \frac{T_2}{T_1} = 100000 \times \frac{673.15}{293.15} \approx 229630 \, \text{Pa} \);
Convert back to kPa: \( P_2 = 229630 / 1000 = 229.63000 \, \text{kPa} \);
Result: \( P_2 = 229.63000 \, \text{kPa} \). [Ref web ID: 0]

Example 2 (Solving for Final Temperature): Calculate \( T_2 \) for a gas in a rigid container with the following properties:

Initial Pressure: \( P_1 = 1.6 \, \text{atm} \);
Initial Temperature: \( T_1 = 460 \, \text{K} \);
Final Pressure: \( P_2 = 1 \, \text{atm} \);
Convert pressures to Pa: \( P_1 = 1.6 \times 101325 = 162120 \, \text{Pa} \), \( P_2 = 1 \times 101325 = 101325 \, \text{Pa} \);
Final Temperature: \( T_2 = T_1 \times \frac{P_2}{P_1} = 460 \times \frac{101325}{162120} = 287.5 \, \text{K} \);
Result: \( T_2 = 287.50000 \, \text{K} \). [Ref web ID: 0]

5. Frequently Asked Questions (FAQ)

Q: What does Gay-Lussac's Law represent?
A: Gay-Lussac's Law states that the pressure of an ideal gas is directly proportional to its absolute temperature when volume and mass are constant, meaning if temperature increases, pressure increases proportionally, and vice versa.

Q: Why must temperature be in Kelvin?
A: The law requires absolute temperature (Kelvin) because it is directly proportional to pressure. Using Celsius or Fahrenheit would introduce incorrect offsets since they are not absolute scales.

Q: Can this calculator be used for any gas?
A: The calculator assumes the gas behaves as an ideal gas. Real gases may deviate from this behavior under extreme conditions (e.g., very high pressures or low temperatures), but for most practical scenarios, the law provides a good approximation.