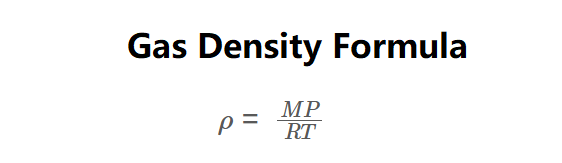Gas Density Calculator

Molar Mass (\( M \)):

Pressure (\( P \)):

Temperature (\( T \)):

Density (\( \rho \)):

1. What is the Gas Density Calculator?

Definition: This calculator computes the density (\( \rho \)) of a gas based on its molar mass (\( M \)), pressure (\( P \)), and temperature (\( T \)).

Purpose: It is used in physics, chemistry, and engineering to determine gas properties for applications like aerodynamics and thermodynamics.

2. How Does the Calculator Work?

The calculator uses the formula derived from the ideal gas law:

\( \rho = \frac{MP}{RT} \)

Where:

\( \rho \): Density (kg/m³, lb/cu ft, lb/cu yd, g/cm³, kg/cm³, mg/cm³, g/m³, g/dm³, g/L);
\( M \): Molar mass (g/mol, µg, mg, g, dag, kg, gr, dr, oz, lb);
\( P \): Pressure (µPa, mPa, Pa, bar, psi, atm, hPa, kPa, MPa, GPa);
\( R \): Universal gas constant (\( 8.314462618 \, \text{J·mol}^{-1}\text{K}^{-1} \));
\( T \): Temperature (K, °C, °F).

Steps:

Enter the molar mass (\( M \)) with its unit.
Enter the pressure (\( P \)) with its unit.
Enter the temperature (\( T \)) with its unit.
Convert molar mass to kg/mol, pressure to Pa, and temperature to Kelvin.
Calculate the density using \( \rho = \frac{MP}{RT} \).
Convert the result to the selected output unit.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Gas Density Calculation

Calculating gas density is crucial for:

Chemistry: Determining gas behavior in reactions.
Engineering: Designing HVAC systems and gas storage.
Physics: Studying fluid dynamics and thermodynamics.

4. Using the Calculator

Example 1: Calculate the density with \( M = 28 \, \text{g/mol} \), \( P = 10 \, \text{Pa} \), \( T = 50 \, \text{K} \):

Molar Mass: \( M = 28 \, \text{g/mol} \div 1000 = 0.028 \, \text{kg/mol} \);
Pressure: \( P = 10 \, \text{Pa} \);
Temperature: \( T = 50 \, \text{K} \);
Density: \( \rho = \frac{0.028 \cdot 10}{8.314462618 \cdot 50} \approx 0.000673 \, \text{kg/m}^3 \);
Result (in kg/m³): \( \rho = 6.7300 \times 10^{-4} \, \text{kg/m}^3 \).

Example 2: Calculate the density with \( M = 32 \, \text{g} \), \( P = 1 \, \text{atm} \), \( T = 25 \, \text{°C} \):

Molar Mass: \( M = 32 \, \text{g} \div 1000 = 0.032 \, \text{kg} \) (interpreted as per mole implicitly);
Pressure: \( P = 1 \, \text{atm} \times 101325 = 101325 \, \text{Pa} \);
Temperature: \( T = 25 \, \text{°C} + 273.15 = 298.15 \, \text{K} \);
Density: \( \rho = \frac{0.032 \cdot 101325}{8.314462618 \cdot 298.15} \approx 1.308 \, \text{kg/m}^3 \);
Result (in g/L): \( \rho = 1.3080 \, \text{g/L} \).

5. Frequently Asked Questions (FAQ)

Q: What is gas density?
A: Gas density (\( \rho \)) is the mass per unit volume of a gas, typically expressed in kg/m³ or g/L.

Q: Why does temperature need to be in Kelvin?
A: The ideal gas law requires absolute temperature in Kelvin to ensure accurate calculations.

Q: Does this calculator apply to real gases?
A: This calculator uses the ideal gas law, which is an approximation. Real gases may deviate under high pressure or low temperature.