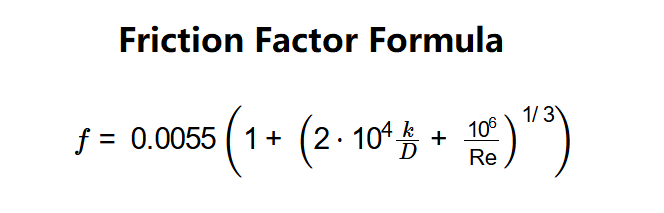Friction Factor Calculator

Hydraulic Diameter (\( D \)):

Surface Roughness (\( k \)):

Reynolds Number (\( \text{Re} \)):

1. What is Friction Factor Calculator?

Definition: This calculator computes the Darcy friction factor (\( f \)) for fluid flow in a pipe using Moody's approximation to the Colebrook-White equation, based on the hydraulic diameter, surface roughness, and Reynolds number.

Purpose: It is used in fluid dynamics and engineering to determine the friction factor, which is essential for calculating pressure losses in pipes, aiding in the design and analysis of piping systems such as in HVAC, water distribution, and industrial processes.

2. How Does the Calculator Work?

The calculator uses the following formula for Moody's approximation:

\( f = 0.0055 \left( 1 + \left( 2 \cdot 10^4 \frac{k}{D} + \frac{10^6}{\text{Re}} \right)^{1/3} \right) \)

Where:

\( f \): Darcy friction factor (dimensionless);
\( k \): Surface roughness (m);
\( D \): Hydraulic diameter (m);
\( \text{Re} \): Reynolds number (dimensionless).

Steps:

Enter the hydraulic diameter (\( D \)) with its unit.
Enter the surface roughness (\( k \)) with its unit.
Enter the Reynolds number (\( \text{Re} \)).
Convert \( D \) and \( k \) to meters.
Validate: \( \text{Re} \) must be between 4,000 and 5 × 10⁸, and \( k/D \) must be less than 0.01.
Calculate the friction factor: \( f = 0.0055 \left( 1 + \left( 2 \cdot 10^4 \frac{k}{D} + \frac{10^6}{\text{Re}} \right)^{1/3} \right) \).
Display the friction factor, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 5 decimal places.

3. Importance of Friction Factor Calculation

Calculating the friction factor is crucial for:

Pressure Loss Calculation: Determining the pressure drop in pipes due to friction, which is essential for pump sizing and system design.
System Efficiency: Optimizing pipe design to minimize energy losses due to friction in fluid transport systems.
Performance Analysis: Evaluating the performance of piping systems in various applications, such as water supply, oil pipelines, and HVAC systems.

4. Using the Calculator

Example 1: Calculate \( f \) for a pipe with the following properties:

Hydraulic Diameter: \( D = 0.1 \, \text{m} \);
Surface Roughness: \( k = 0.00015 \, \text{m} \);
Reynolds Number: \( \text{Re} = 200,000 \);
Check: \( \text{Re} = 200,000 \) (within range), \( k/D = 0.00015 / 0.1 = 0.0015 < 0.01 \);
Friction Factor: \( f = 0.0055 \left( 1 + \left( 2 \cdot 10^4 \times 0.0015 + \frac{10^6}{200,000} \right)^{1/3} \right) = 0.0055 \left( 1 + (30 + 5)^{1/3} \right) \approx 0.023 \);
Result: \( f = 0.02300 \).

Example 2 (Different Units): Calculate \( f \) with the following properties:

Hydraulic Diameter: \( D = 50 \, \text{mm} \);
Convert \( D \): \( D = 50 / 1000 = 0.05 \, \text{m} \);
Surface Roughness: \( k = 0.1 \, \text{mm} \);
Convert \( k \): \( k = 0.1 / 1000 = 0.0001 \, \text{m} \);
Reynolds Number: \( \text{Re} = 111,112 \);
Check: \( \text{Re} = 111,112 \) (within range), \( k/D = 0.0001 / 0.05 = 0.002 < 0.01 \);
Friction Factor: \( f = 0.0055 \left( 1 + \left( 2 \cdot 10^4 \times 0.002 + \frac{10^6}{111,112} \right)^{1/3} \right) = 0.0055 \left( 1 + (40 + 9)^{1/3} \right) \approx 0.023 \);
Result: \( f = 0.02337 \).

5. Frequently Asked Questions (FAQ)

Q: What is the Darcy friction factor?
A: The Darcy friction factor (\( f \)) is a dimensionless quantity used in fluid dynamics to quantify the frictional resistance to flow in a pipe, used in the Darcy-Weisbach equation for pressure loss.

Q: Why is the Reynolds number important?
A: The Reynolds number (\( \text{Re} \)) determines the flow regime (laminar, transitional, or turbulent). Moody's approximation is valid for turbulent flow (\( \text{Re} \) between 4,000 and 5 × 10⁸).

Q: What if my flow is not turbulent?
A: This calculator uses Moody's approximation, which is valid for turbulent flow. For laminar flow (\( \text{Re} < 2,000 \)), the friction factor can be calculated as \( f = 64 / \text{Re} \). For transitional flow, a more complex method like the Colebrook-White equation is needed.