Frequency of Light Calculator

1. What is the Frequency of Light Calculator?

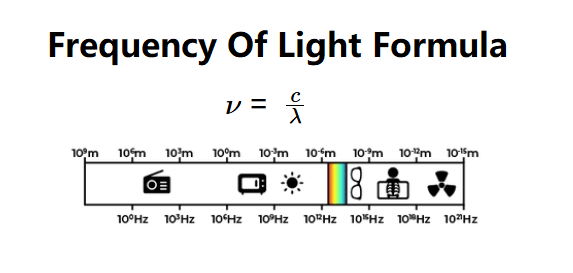
Definition: This calculator computes the frequency (\( \nu \)) of light based on its wavelength (\( \lambda \)) using the relationship between the speed of light, frequency, and wavelength.

Purpose: It is used in optics and physics to determine the frequency of electromagnetic waves, such as visible light, X-rays, or radio waves, given their wavelength.

2. How Does the Calculator Work?

The calculator uses the following equation:

\( \nu = \frac{c}{\lambda} \)

Where:

\( \nu \): Frequency (Hz, kHz, MHz, GHz, THz);
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \));
\( \lambda \): Wavelength (m, cm, mm, nm, pm, Å).

Steps:

Enter the wavelength (\( \lambda \)) with its unit.
Convert the wavelength to meters.
Calculate the frequency: \( \nu = \frac{c}{\lambda} \).
Convert the frequency to the selected output unit and display, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Frequency of Light Calculation

Calculating the frequency of light is crucial for:

Optics: Understanding the properties of light in different regions of the electromagnetic spectrum.
Spectroscopy: Analyzing the spectral lines of elements and molecules.
Telecommunications: Designing systems that use specific frequencies of light, such as in fiber optics.

4. Using the Calculator

Example 1: Calculate the frequency of visible light with a wavelength of 500 nm:

Wavelength: \( \lambda = 500 \, \text{nm} = 5 \times 10^{-7} \, \text{m} \);
Frequency: \( \nu = \frac{299,792,458}{5 \times 10^{-7}} = 5.996 \times 10^{14} \, \text{Hz} \);
Result: \( \nu = 5.9960 \times 10^{14} \, \text{Hz} \) or \( 599.6000 \, \text{THz} \).

Example 2 (Different Wavelength): Calculate the frequency of an X-ray with a wavelength of 1 Å:

Wavelength: \( \lambda = 1 \, \text{Å} = 1 \times 10^{-10} \, \text{m} \);
Frequency: \( \nu = \frac{299,792,458}{1 \times 10^{-10}} = 2.998 \times 10^{18} \, \text{Hz} \);
Result: \( \nu = 2.9980 \times 10^{18} \, \text{Hz} \) or \( 2.9980 \times 10^6 \, \text{THz} \).

5. Frequently Asked Questions (FAQ)

Q: What does the frequency of light tell us?
A: The frequency determines the energy of the photons (\( E = h \nu \)) and the type of electromagnetic radiation (e.g., visible light, X-rays, radio waves).

Q: Why does a shorter wavelength result in a higher frequency?
A: Frequency and wavelength are inversely proportional (\( \nu \propto \frac{1}{\lambda} \)). A shorter wavelength means the light wave oscillates more times per second, increasing the frequency.

Q: Can this calculator be used for light in a medium?
A: This calculator assumes light travels in a vacuum (\( c = 299,792,458 \, \text{m/s} \)). In a medium, the speed of light is slower, and the equation would need to be adjusted (\( \nu = \frac{v}{\lambda} \), where \( v \) is the speed in the medium).