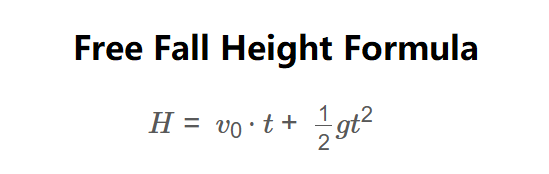Free Fall Height Calculator

Gravitational Acceleration (\( g \)):

Initial Velocity (\( v_0 \)):

Time of Fall (\( t \)):

1. What is the Free Fall Height Calculator?

Definition: This calculator computes the height (\( H \)) an object falls under free fall conditions, based on gravitational acceleration (\( g \)), initial velocity (\( v_0 \)), and time of fall (\( t \)).

Purpose: It is used in physics, engineering, and education to determine the distance fallen by an object under gravity.

2. How Does the Calculator Work?

The calculator uses the formula:

\( H = v_0 \cdot t + \frac{1}{2} g t^2 \)

Where:

\( g \): Gravitational acceleration (m/s², ft/s²);
\( v_0 \): Initial velocity (m/s, km/h, ft/s, mph, kn, km/s, mi/s, ft/min, m/min);
\( t \): Time of fall (s, min);
\( H \): Height fallen (cm, m, km, in, ft, yd, mi).

Steps:

Enter the gravitational acceleration (\( g \)) with its unit.
Enter the initial velocity (\( v_0 \)) with its unit.
Enter the time of fall (\( t \)) with its unit.
Convert all inputs to base SI units (m/s² for \( g \), m/s for \( v_0 \), s for \( t \)).
Calculate the height using \( H = v_0 \cdot t + \frac{1}{2} g t^2 \).
Convert the result to the selected output unit.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Free Fall Height Calculation

Calculating free fall height is crucial for:

Physics Education: Understanding gravitational motion.
Engineering Safety: Designing fall protection systems.
Sports Science: Analyzing jumps and drops.

4. Using the Calculator

Example 1: Calculate the height fallen with \( g = 9.81 \, \text{m/s}^2 \), \( v_0 = 0 \, \text{m/s} \), and \( t = 2 \, \text{s} \):

Gravitational Acceleration: \( g = 9.81 \, \text{m/s}^2 \);
Initial Velocity: \( v_0 = 0 \, \text{m/s} \);
Time: \( t = 2 \, \text{s} \);
Height: \( H = 0 \cdot 2 + \frac{1}{2} \cdot 9.81 \cdot 2^2 = 19.62 \, \text{m} \);
Result (in meters): \( H = 19.6200 \, \text{m} \).

Example 2: Calculate the height fallen with \( g = 32.2 \, \text{ft/s}^2 \), \( v_0 = 10 \, \text{km/h} \), and \( t = 1 \, \text{min} \):

Gravitational Acceleration: \( g = 32.2 \, \text{ft/s}^2 \times 0.3048 = 9.81856 \, \text{m/s}^2 \);
Initial Velocity: \( v_0 = 10 \, \text{km/h} \times 0.277778 = 2.77778 \, \text{m/s} \);
Time: \( t = 1 \, \text{min} \times 60 = 60 \, \text{s} \);
Height: \( H = 2.77778 \cdot 60 + \frac{1}{2} \cdot 9.81856 \cdot 60^2 = 166.6668 + 17673.648 = 17840.3148 \, \text{m} \);
Result (in feet): \( H = 58530.0588 \, \text{ft} \).

5. Frequently Asked Questions (FAQ)

Q: What is free fall height?
A: Free fall height is the distance an object falls under gravity, accounting for any initial velocity.

Q: What happens if the initial velocity is zero?
A: The formula simplifies to \( H = \frac{1}{2} g t^2 \), as the object is dropped from rest.

Q: Does this calculator account for air resistance?
A: No, this calculator assumes ideal conditions with no air resistance.