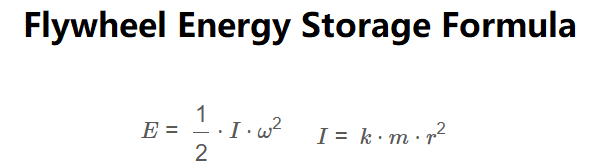Flywheel Energy Storage Calculator (Energy Only)

Mass (\( m \)):

Reference Radius (\( r \)):

Geometric Constant (\( k \)):

Angular Velocity (\( \omega \)):

1. What is a Flywheel Energy Storage Calculator?

Definition: This calculator computes the rotational energy (\(E\)) stored in a flywheel, based on its mass, radius, shape, and angular velocity.

Purpose: It is used in engineering to design and analyze flywheel energy storage systems, which store energy as rotational kinetic energy and can release it as needed.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Rotational Energy: \[ E = \frac{1}{2} \cdot I \cdot \omega^2 \] Moment of Inertia: \[ I = k \cdot m \cdot r^2 \] Where:

\( E \): Rotational energy (J, kJ, MJ, Wh)
\( I \): Moment of inertia (kg·m²)
\( \omega \): Angular velocity (rad/s, rpm, Hz)
\( k \): Geometric constant (dimensionless, depends on shape)
\( m \): Mass (mg, g, dag, kg, oz, lb, st, Earth)
\( r \): Reference radius (mm, cm, m, in, ft, yd)

Geometric Constants (\( k \)):

Rim-loaded wheel: \( k = 1.000 \)
Flat solid disk: \( k = 0.606 \)
Flat hollow disk: \( k = 0.333 \)
Solid sphere: \( k = 0.400 \)
Thin rim hollow cylinder: \( k = 1.000 \)

Unit Conversions:

Mass (\( m \)): mg (1 mg = 0.000001 kg), g (1 g = 0.001 kg), dag (1 dag = 0.01 kg), kg, oz (1 oz = 0.028349523125 kg), lb (1 lb = 0.45359237 kg), st (1 st = 6.35029318 kg), Earth (1 Earth = 5.972 × 10²⁴ kg)
Radius (\( r \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
Angular Velocity (\( \omega \)): rad/s, rpm (1 rpm = \( \frac{2\pi}{60} \) rad/s ≈ 0.104719755 rad/s), Hz (1 Hz = \( 2\pi \) rad/s ≈ 6.283185307 rad/s)
Energy (\( E \)): J, kJ (1 kJ = 1000 J), MJ (1 MJ = 1000000 J), Wh (1 Wh = 3600 J)

Steps:

Enter the mass, radius, geometric constant, and angular velocity, and select their units.
Convert mass to kg, radius to m, and angular velocity to rad/s for calculations.
Calculate the moment of inertia and then the stored energy.
Display the result, allowing unit selection for energy.

3. Importance of Flywheel Energy Storage Calculation

Calculating flywheel energy storage is crucial for:

Energy Storage Systems: Designing efficient flywheel systems for storing and releasing energy in applications like power grids or vehicles.
Engineering Design: Optimizing the flywheel’s shape and mass to maximize energy storage capacity.
Physics Education: Understanding the principles of rotational kinetic energy and its applications.

4. Using the Calculator

Examples:

Example 1: For \( m = 7500 \, \text{kg} \), \( r = 1.0926 \, \text{m} \), \( k = 0.606 \), \( \omega = 175 \, \text{rpm} \), energy in Wh:
- Moment of Inertia: \( I = 0.606 \times 7500 \times (1.0926)^2 = 5425.935 \, \text{kg·m}^2 \)
- Angular Velocity: \( \omega = 175 \times \frac{2 \pi}{60} = 18.325957 \, \text{rad/s} \)
- Stored Energy: \( E = \frac{1}{2} \times 5425.935 \times (18.325957)^2 = 911405.5 \, \text{J} \), \( E = 911405.5 \div 3600 = 253.168 \, \text{Wh} \)
Example 2: For \( m = 10 \, \text{kg} \), \( r = 0.5 \, \text{m} \), \( k = 1.000 \), \( \omega = 1200 \, \text{rpm} \), energy in kJ:
- Moment of Inertia: \( I = 1.000 \times 10 \times (0.5)^2 = 2.500 \, \text{kg·m}^2 \)
- Angular Velocity: \( \omega = 1200 \times \frac{2 \pi}{60} = 125.6637 \, \text{rad/s} \)
- Stored Energy: \( E = \frac{1}{2} \times 2.500 \times (125.6637)^2 = 19739.208 \, \text{J} \), \( E = 19739.208 \times 0.001 = 19.739 \, \text{kJ} \)

5. Frequently Asked Questions (FAQ)

Q: What is flywheel energy storage?
A: Flywheel energy storage involves storing energy in the form of rotational kinetic energy in a spinning flywheel, which can be released as needed for various applications.

Q: What does the geometric constant (\(k\)) represent?
A: The geometric constant (\(k\)) depends on the shape of the flywheel and affects its moment of inertia. Common values include 0.606 for a flat solid disk and 0.333 for a flat hollow disk.

Q: How is angular velocity converted to rad/s?
A: Angular velocity in rad/s is calculated as \( \omega \, (\text{rad/s}) = 2 \pi \cdot \omega \, (\text{Hz}) \) or \( \omega \, (\text{rad/s}) = \frac{2 \pi}{60} \cdot \omega \, (\text{rpm}) \).