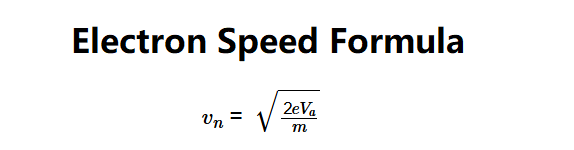Electron Speed Calculator

1. What is Electron Speed Calculator?

Definition: This calculator computes the classical (non-relativistic) speed (\( v_n \)) of an electron accelerated by an electric field, based on the accelerating potential (\( V_a \)).

Purpose: It is used in physics to determine the speed of electrons in applications like electron guns, cathode ray tubes, and particle accelerators, assuming non-relativistic conditions.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula:

\( v_n = \sqrt{\frac{2 e V_a}{m}} \)

Where:

\( v_n \): Classical speed of the electron (m/s, km/s, km/h, mph, ft/s, fraction of c)
\( e \): Elementary charge (\( 1.602 \times 10^{-19} \, \text{C} \))
\( V_a \): Accelerating potential (V, kV, MV)
\( m \): Mass of an electron (\( 9.109 \times 10^{-31} \, \text{kg} \))

Unit Conversions:

Accelerating Potential (\( V_a \)):
- 1 V = 1 V
- 1 kV = \( 10^3 \) V
- 1 MV = \( 10^6 \) V
Speed (\( v_n \)):
- 1 m/s = 1 m/s
- 1 km/s = 1000 m/s
- 1 km/h = \( \frac{1000}{3600} \) m/s
- 1 mph = \( \frac{1609.344}{3600} \) m/s
- 1 ft/s = \( \frac{1}{3.28084} \) m/s
- 1 c = \( 299,792,458 \) m/s

Steps:

Enter the accelerating potential (\( V_a \)) with its respective unit (V, kV, MV).
Convert the accelerating potential to volts.
Calculate the electron speed using \( v_n = \sqrt{\frac{2 e V_a}{m}} \).
Select the desired unit for the speed result (m/s, km/s, km/h, mph, ft/s, fraction of c).
Convert the speed to the selected unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Electron Speed Calculation

Calculating the speed of an electron in an electric field is crucial for:

Electron Optics: Understanding electron speeds is essential for designing electron guns and cathode ray tubes used in older televisions and oscilloscopes.
Particle Accelerators: The non-relativistic speed calculation provides a starting point for understanding electron behavior in accelerators before relativistic effects become significant.
Physics Education: It helps students learn about the relationship between electric potential, kinetic energy, and velocity in classical physics.

4. Using the Calculator

Examples:

Example 1: Calculate the speed of an electron accelerated by a potential of 100 V, with the result in ft/s:
- Enter \( V_a = 100 \) V.
- \( v_n = \sqrt{\frac{2 \times 1.602 \times 10^{-19} \times 100}{9.109 \times 10^{-31}}} \approx 5.93 \times 10^6 \) m/s
- Convert to ft/s: \( v_n = 5.93 \times 10^6 \times 3.28084 \approx 1.946 \times 10^7 \) ft/s
- Result: \( v_n = 1.9460e7 \) ft/s
Example 2: Calculate the speed of an electron accelerated by a potential of 1 kV, with the result in km/s:
- Enter \( V_a = 1 \) kV.
- Convert to volts: \( V_a = 1 \times 10^3 = 1000 \) V.
- \( v_n = \sqrt{\frac{2 \times 1.602 \times 10^{-19} \times 1000}{9.109 \times 10^{-31}}} \approx 1.876 \times 10^7 \) m/s
- Convert to km/s: \( v_n = 1.876 \times 10^7 / 1000 \approx 1.876 \times 10^4 \) km/s
- Result: \( v_n = 18760.0000 \) km/s

5. Frequently Asked Questions (FAQ)

Q: What is the classical speed of an electron?
A: The classical speed of an electron is the velocity calculated using non-relativistic physics, assuming the electron's speed is much less than the speed of light.

Q: Why is this calculation non-relativistic?
A: The formula used assumes that the electron's speed is low enough that relativistic effects (like mass increase) are negligible. For high potentials, the speed may approach the speed of light, requiring a relativistic calculation.

Q: What happens if the calculated speed exceeds the speed of light?
A: The calculator will display an error, as the non-relativistic formula is not valid for speeds approaching or exceeding the speed of light (\( 299,792,458 \, \text{m/s} \)).