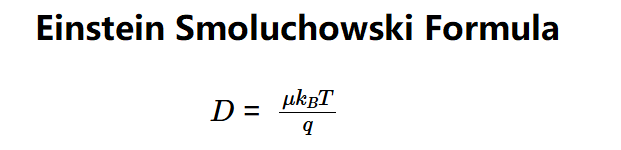Electrical Mobility Calculator

Electrical Mobility (\( \mu \)):

Temperature (\( T \)):

Charge of Carriers (\( q \)):

1. What is Electrical Mobility Calculator?

Definition: This calculator computes the diffusion constant (\( D \)) using the Einstein-Smoluchowski relation, based on electrical mobility, temperature, and charge of the carriers.

Purpose: It is used in physics and materials science to relate the mobility of charged particles (like electrons or ions) to their diffusion behavior, which is crucial in semiconductors, electrolytes, and other systems.

2. How Does the Calculator Work?

The calculator uses the following formula:

\( D = \frac{\mu k_B T}{q} \)

Where:

\( D \): Diffusion constant (m²/s);
\( \mu \): Electrical mobility (m²/(V·s));
\( k_B \): Boltzmann constant (\( 1.3806503 \times 10^{-23} \, \text{J/K} \));
\( T \): Temperature (K);
\( q \): Charge of the carriers (C).

Steps:

Enter the electrical mobility (\( \mu \)) with its unit.
Enter the temperature (\( T \)) with its unit.
Enter the charge of the carriers (\( q \)) with its unit.
Convert all inputs to base units (m²/(V·s) for mobility, K for temperature, C for charge).
Calculate the diffusion constant: \( D = \frac{\mu k_B T}{q} \).
Convert the diffusion constant to the selected output unit and display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 5 decimal places.

3. Importance of Electrical Mobility Calculation

Calculating the diffusion constant using the Einstein-Smoluchowski relation is crucial for:

Semiconductor Design: Understanding how charge carriers move in materials, which affects the performance of transistors and diodes.
Electrolyte Analysis: Studying ion transport in batteries and fuel cells to improve efficiency.
Material Science: Analyzing diffusion processes in solids, liquids, and gases for applications like sensors and nanotechnology.

4. Using the Calculator

Example 1: Calculate \( D \) for an electron with the following properties:

Electrical Mobility: \( \mu = 0.135 \, \text{m}^2/(\text{V·s}) \);
Temperature: \( T = 300 \, \text{K} \);
Charge: \( q = 1 \, \text{elementary charge} = 1.60217662 \times 10^{-19} \, \text{C} \);
Boltzmann Constant: \( k_B = 1.3806503 \times 10^{-23} \, \text{J/K} \);
Diffusion Constant: \( D = \frac{0.135 \times (1.3806503 \times 10^{-23}) \times 300}{1.60217662 \times 10^{-19}} \approx 3.489 \times 10^{-3} \, \text{m}^2/\text{s} \);
Result (in mm²/s): \( D = 3.489 \times 10^{-3} \times 10^6 = 3.489 \, \text{mm}^2/\text{s} \).

Example 2 (Different Units): Calculate \( D \) with the following properties:

Electrical Mobility: \( \mu = 1500 \, \text{mm}^2/(\text{V·s}) \);
Temperature: \( T = 77 \, \text{°F} \);
Charge: \( q = 1 \, \text{mAh} \);
Convert units: \( \mu = 1500 \times 10^{-6} = 0.0015 \, \text{m}^2/(\text{V·s}) \), \( T = (77 - 32) \times 5/9 + 273.15 = 298.15 \, \text{K} \), \( q = 1 \times 3.6 = 3.6 \, \text{C} \);
Diffusion Constant: \( D = \frac{0.0015 \times (1.3806503 \times 10^{-23}) \times 298.15}{3.6} \approx 1.717 \times 10^{-6} \, \text{m}^2/\text{s} \);
Result (in mm²/s): \( D = 1.717 \times 10^{-6} \times 10^6 = 0.00172 \, \text{mm}^2/\text{s} \).

5. Frequently Asked Questions (FAQ)

Q: What does electrical mobility represent?
A: Electrical mobility (\( \mu \)) measures how quickly a charged particle moves in an electric field, defined as the drift velocity per unit electric field strength.

Q: Why does temperature affect the diffusion constant?
A: Temperature (\( T \)) is directly proportional to the diffusion constant in the Einstein-Smoluchowski relation. Higher temperatures increase the thermal energy of particles, leading to faster diffusion.

Q: Can this calculator be used for any charged particle?
A: Yes, the Einstein-Smoluchowski relation applies to any charged particle (e.g., electrons, ions) as long as the mobility, temperature, and charge are known.