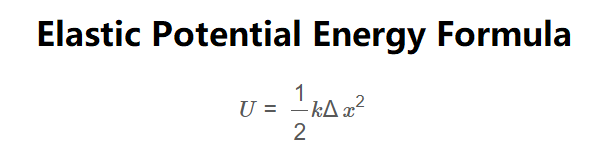Elastic Potential Energy Calculator

1. What is an Elastic Potential Energy Calculator?

Definition: This calculator determines the elastic potential energy stored in a spring based on its spring constant and deformation.

Purpose: It is used in physics to calculate the energy stored in a spring when it is stretched or compressed.

2. How Does the Calculator Work?

The calculator uses the following formula:

\[ U = \frac{1}{2} k \Delta x^2 \] Where:

\(U\): Elastic potential energy (J, kJ, MJ, Wh, kWh, ft-lb, kcal)
\(k\): Spring constant (N/m, N/cm, N/mm)
\(\Delta x\): Deformation (stretch or compression) of the spring (m, cm, mm)

Unit Conversions:

Spring Constant (k): N/m, N/cm (1 N/cm = 100 N/m), N/mm (1 N/mm = 1000 N/m)
Deformation (\(\Delta x\)): m, cm (1 cm = 0.01 m), mm (1 mm = 0.001 m)
Energy (U): J, kJ (1 J = 0.001 kJ), MJ (1 J = 0.000001 MJ), Wh (1 J = 1/3600 Wh), kWh (1 J = 1/3600000 kWh), ft-lb (1 J = 0.73756214927727 ft-lb), kcal (1 J = 1/4184 kcal)

Steps:

Enter the spring constant (k), selecting the unit (N/m, N/cm, N/mm).
Enter the deformation (\(\Delta x\)), selecting the unit (m, cm, mm).
Convert all inputs to base units (N/m, m) for calculation.
Calculate the elastic potential energy using the formula.
Convert the result to the selected energy unit (J, kJ, MJ, Wh, kWh, ft-lb, kcal) and display.

3. Importance of Elastic Potential Energy Calculation

Calculating elastic potential energy is crucial for:

Physics Education: Understanding energy storage in springs.
Engineering: Designing mechanical systems involving springs.
Applications: Analyzing systems like suspension systems or spring-loaded devices.

4. Using the Calculator

Examples:

Example 1: For \(k = 200 \, \text{N/m}\), \(\Delta x = 0.1 \, \text{m}\):
- Energy: \(U = \frac{1}{2} \times 200 \times 0.1^2 = 1 \, \text{J}\)
- In kJ: \(U = 1 \times 0.001 = 0.001 \, \text{kJ}\)
- In ft-lb: \(U = 1 \times 0.73756214927727 = 0.738 \, \text{ft-lb}\)
Example 2: For \(k = 50 \, \text{N/cm}\), \(\Delta x = 5 \, \text{cm}\):
- Convert: \(k = 50 \times 100 = 5000 \, \text{N/m}\), \(\Delta x = 5 \times 0.01 = 0.05 \, \text{m}\)
- Energy: \(U = \frac{1}{2} \times 5000 \times 0.05^2 = 6.25 \, \text{J}\)
- In MJ: \(U = 6.25 \times 0.000001 = 0.00000625 \, \text{MJ}\)
- In Wh: \(U = 6.25 \times (1/3600) = 0.001736 \, \text{Wh}\)

5. Frequently Asked Questions (FAQ)

Q: What is elastic potential energy?
A: Elastic potential energy is the energy stored in a spring when it is stretched or compressed, calculated as \(U = \frac{1}{2} k \Delta x^2\).

Q: What is the spring constant?
A: The spring constant (\(k\)) is a proportionality constant that describes the relationship between the force applied to a spring and its deformation.

Q: Can the spring constant be negative?
A: No, the spring constant must be positive, as it represents a physical property of the spring.

Favorite