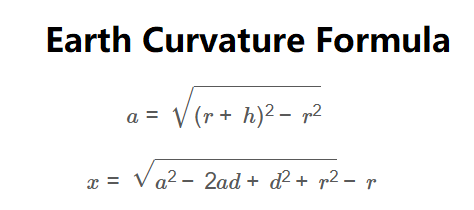Earth Curvature Calculator

Distance to Horizon (\( a \)):

Obstructed Height (\( x \)):

1. What is Earth Curvature Calculator?

Definition: This calculator computes the height of the obstructed part (\( x \)) of an object due to the Earth's curvature, given the observer's eyeshot level and the distance to the object.

Purpose: It is used to determine how much of a distant object is hidden below the horizon due to the Earth's curvature, useful in navigation, surveying, and understanding visibility limits.

2. How Does the Calculator Work?

The calculator uses two formulas:

Formula 1 (Distance to Horizon): \[ a = \sqrt{(r + h)^2 - r^2} \] Formula 2 (Obstructed Height): \[ x = \sqrt{a^2 - 2ad + d^2 + r^2} - r \] Where:

\( a \): Distance to the horizon (m, km, mi, ft)
\( x \): Height of the obstructed part of the object (m, km, mi, ft)
\( r \): Earth's radius, 3959 mi (6371 km)
\( h \): Observer's eyeshot level above mean sea level (m, km, mi, ft)
\( d \): Distance to the object (m, km, mi)

Unit Conversions:

Height (\( h \)) and Distance (\( d \)): m (1 m = 0.000621371 mi), km (1 km = 0.621371 mi), mi, ft (1 ft = 0.000189394 mi)
Distance to Horizon (\( a \)) and Obstructed Height (\( x \)): m (1 mi = 1609.344 m), km (1 mi = 1.609344 km), mi, ft (1 mi = 5280 ft)

Steps:

Enter the observer's eyeshot level (\( h \)) and the distance to the object (\( d \)), and select their units.
Convert \( h \) and \( d \) to miles (base unit for calculation).
Calculate the distance to the horizon \( a = \sqrt{(r + h)^2 - r^2} \).
Calculate the obstructed height \( x = \sqrt{a^2 - 2ad + d^2 + r^2} - r \).
Convert \( a \) and \( x \) to the selected units (m, km, mi, ft).
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Earth Curvature Calculation

Calculating the obstructed height due to Earth's curvature is crucial for:

Navigation: Determining how much of a distant object (e.g., a ship or mountain) is hidden below the horizon.
Surveying: Accounting for curvature in long-distance measurements on Earth's surface.
Education: Understanding the effects of Earth's curvature on visibility and line-of-sight calculations.

4. Using the Calculator

Examples:

Example 1: For \( h = 6 \, \text{ft} \), \( d = 25 \, \text{mi} \), distance to horizon in miles, obstructed height in miles:
- Convert: \( h = 6 \times 0.000189394 = 0.0011364 \, \text{mi} \)
- Distance to horizon: \( a = \sqrt{(3959 + 0.0011364)^2 - 3959^2} \approx 3.0000 \, \text{mi} \)
- Obstructed height: \( x = \sqrt{3^2 - 2 \times 3 \times 25 + 25^2 + 3959^2} - 3959 \approx 0.0611 \, \text{mi} \)
Example 2: For \( h = 1.8 \, \text{m} \), \( d = 10 \, \text{km} \), distance to horizon in km, obstructed height in feet:
- Convert: \( h = 1.8 \times 0.000621371 = 0.00111847 \, \text{mi} \), \( d = 10 \times 0.621371 = 6.21371 \, \text{mi} \)
- Distance to horizon: \( a = \sqrt{(3959 + 0.00111847)^2 - 3959^2} \approx 2.976 \, \text{mi} \), in km: \( 2.976 \times 1.609344 \approx 4.7894 \, \text{km} \)
- Obstructed height: \( x = \sqrt{2.976^2 - 2 \times 2.976 \times 6.21371 + 6.21371^2 + 3959^2} - 3959 \approx 0.0098 \, \text{mi} \), in ft: \( 0.0098 \times 5280 \approx 51.7440 \, \text{ft} \)

5. Frequently Asked Questions (FAQ)

Q: What does the obstructed height represent?
A: The obstructed height (\( x \)) is the portion of a distant object that is hidden below the horizon due to the Earth's curvature.

Q: Why is the Earth's radius fixed at 3959 miles?
A: The calculator uses 3959 miles (6371 km) as the Earth's mean radius for simplicity, as provided in the example. The Earth's actual shape is slightly ellipsoidal, but this value is a good approximation.

Q: How does the distance to the object affect the obstructed height?
A: A greater distance to the object increases the obstructed height, as more of the object is hidden by the Earth's curvature.