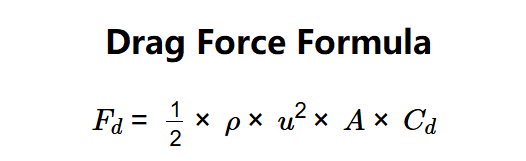1. What is Drag Force Calculator?
Definition: This calculator computes the drag force (\( F_d \)) experienced by an object moving through a fluid, based on the fluid's density, the object's velocity, reference area, and drag coefficient.
Purpose: It is used in physics, aerodynamics, and engineering to determine the resistive force acting on objects like vehicles, aircraft, or any object moving through air, water, or other fluids, aiding in design and performance analysis.
2. How Does the Calculator Work?
The calculator uses the following formula:
- \( F_d = \frac{1}{2} \times \rho \times u^2 \times A \times C_d \)
Where:
- \( F_d \): Drag force (N);
- \( \rho \): Fluid density (kg/m³);
- \( u \): Relative velocity (m/s);
- \( A \): Reference area (m²);
- \( C_d \): Drag coefficient (dimensionless).
Steps:
- Enter the fluid density (\( \rho \)) by selecting a fluid or entering a custom value with its unit.
- Enter the relative velocity (\( u \)) with its unit.
- Enter the reference area (\( A \)) with its unit.
- Enter the drag coefficient (\( C_d \)).
- Convert \( \rho \) to kg/m³, \( u \) to m/s, and \( A \) to m².
- Calculate the drag force: \( F_d = \frac{1}{2} \times \rho \times u^2 \times A \times C_d \).
- Convert the drag force to the selected output unit and display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 5 decimal places.
3. Importance of Drag Force Calculation
Calculating the drag force is crucial for:
- Aerodynamic Design: Optimizing the shape of vehicles, aircraft, and other objects to reduce drag and improve fuel efficiency.
- Performance Analysis: Evaluating how drag affects the speed and stability of moving objects in fluids like air or water.
- Engineering Applications: Designing structures like bridges or buildings to withstand wind forces, or calculating drag in fluid flow systems.
4. Using the Calculator
Example 1 (Predefined Fluid): Calculate \( F_d \) for a car moving through air with the following properties:
- Fluid: Air (at 15°C, \( \rho = 1.225 \, \text{kg/m}^3 \));
- Relative Velocity: \( u = 100 \, \text{km/h} \);
- Convert \( u \): \( u = 100 / 3.6 = 27.7778 \, \text{m/s} \);
- Reference Area: \( A = 2.5 \, \text{m}^2 \);
- Drag Coefficient: \( C_d = 0.3 \);
- Drag Force: \( F_d = \frac{1}{2} \times 1.225 \times (27.7778)^2 \times 2.5 \times 0.3 = 354.3125 \, \text{N} \);
- Result: \( F_d = 354.31250 \, \text{N} \).
Example 2 (Custom Density, Different Units): Calculate \( F_d \) for an object in a fluid with the following properties:
- Fluid Density: \( \rho = 1 \, \text{g/cm}^3 \);
- Convert \( \rho \): \( \rho = 1 \times 1000 = 1000 \, \text{kg/m}^3 \);
- Relative Velocity: \( u = 5 \, \text{m/s} \);
- Reference Area: \( A = 500 \, \text{cm}^2 \);
- Convert \( A \): \( A = 500 / 10000 = 0.05 \, \text{m}^2 \);
- Drag Coefficient: \( C_d = 1.2 \);
- Drag Force: \( F_d = \frac{1}{2} \times 1000 \times (5)^2 \times 0.05 \times 1.2 = 750 \, \text{N} \);
- Result (in kN): \( F_d = 0.75000 \, \text{kN} \).
5. Frequently Asked Questions (FAQ)
Q: What does the drag coefficient \( C_d \) represent?
A: The drag coefficient (\( C_d \)) is a dimensionless number that quantifies the drag or resistance of an object in a fluid, depending on its shape and surface properties.
Q: Why does drag force depend on the square of velocity?
A: The drag force is proportional to \( u^2 \) because the kinetic energy of the fluid impacting the object increases with the square of the velocity, leading to a quadratic relationship.
Q: Can this calculator be used for both liquids and gases?
A: Yes, this calculator works for both liquids and gases, as long as the appropriate fluid density and drag coefficient are provided. However, for high-speed flows (e.g., near the speed of sound), additional factors like compressibility may need to be considered.
 Home
Home
 Back
Back