Distance to Horizon Calculator

Celestial Body:

Radius of Celestial Body (\( r \)):

Observer Height (\( h \)):

1. What is Distance to Horizon Calculator?

Definition: This calculator computes the distance to the horizon (\( d \)) from an observer's height above the surface of a celestial body, assuming a spherical shape.

Purpose: It is used in navigation, astronomy, and geography to determine how far an observer can see to the horizon on a planet or moon.

2. How Does the Calculator Work?

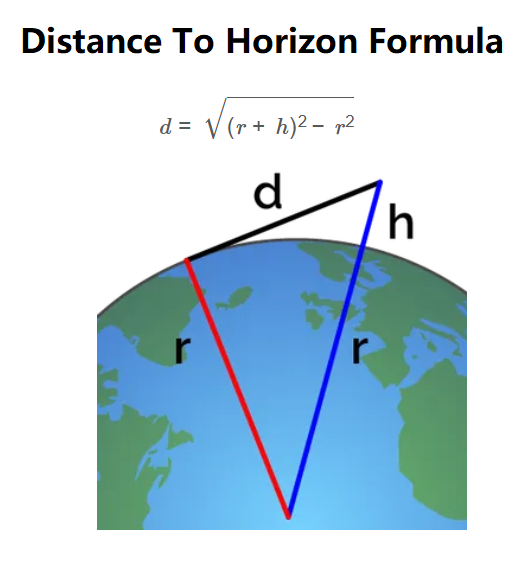
The calculator uses the formula for distance to the horizon:

Formula: \[ d = \sqrt{(r + h)^2 - r^2} \] Where:

\( d \): Distance to the horizon (m, km, mi)
\( r \): Radius of the celestial body (m, km, mi)
\( h \): Height of the observer above the surface (m, km, mi)

Unit Conversions:

Radius (\( r \)) and Height (\( h \)): m, km (1 km = 1000 m), mi (1 mi = 1609.344 m)
Distance (\( d \)): m, km (1 km = 1000 m), mi (1 mi = 1609.344 m)

Steps:

Select a celestial body or enter a custom radius, and specify the observer's height (\( h \)).
Convert \( r \) and \( h \) to meters.
Calculate the distance using \( d = \sqrt{(r + h)^2 - r^2} \).
Convert the result to the selected unit (m, km, mi).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Distance to Horizon Calculation

Calculating the distance to the horizon is crucial for:

Navigation: Determining visibility range for ships, aircraft, or ground-based observers.
Astronomy: Estimating the visible horizon on other celestial bodies for exploration missions.
Education: Understanding the geometry of spherical bodies and line-of-sight calculations.

4. Using the Calculator

Examples:

Example 1: For \( h = 1.75 \, \text{m} \), celestial body = Earth (\( r = 6,371,008 \, \text{m} \)), distance in km:
- Calculate: \( d = \sqrt{(6,371,008 + 1.75)^2 - (6,371,008)^2} \approx 4,722 \, \text{m} \)
- Convert to km: \( d = 4,722 \div 1000 \approx 4.7220 \, \text{km} \)
Example 2: For \( h = 1 \, \text{km} \), celestial body = Moon (\( r = 1,737.4 \, \text{km} \)), distance in km:
- Convert: \( r = 1,737.4 \times 1000 = 1,737,400 \, \text{m} \), \( h = 1 \times 1000 = 1,000 \, \text{m} \)
- Calculate: \( d = \sqrt{(1,737,400 + 1,000)^2 - (1,737,400)^2} \approx 58,983 \, \text{m} \)
- Convert to km: \( d = 58,983 \div 1000 \approx 58.9830 \, \text{km} \)

5. Frequently Asked Questions (FAQ)

Q: What is the distance to the horizon?
A: The distance to the horizon is the straight-line distance from an observer to the farthest point on the surface of a celestial body that is visible, limited by the curvature of the body.

Q: Why does the calculator assume a spherical body?
A: The formula assumes a spherical body for simplicity. While celestial bodies like Earth are slightly ellipsoidal, the difference in the result is minimal for most practical purposes.

Q: How does observer height affect the distance to the horizon?
A: A higher observer height increases the distance to the horizon, as the observer can see farther over the curvature of the body.