Diffraction Grating Calculator

$Diffraction Grating Diagram$

Wavelength ($ \lambda $):

Grating Density (lines/mm):

Angle of Incidence ($ \theta_0 $):

Maximum Order to Calculate:

Diffraction Angles ($ \theta_a $):

Order $ a = 1 $:

Order $ a = 2 $:

Order $ a = 3 $:

Order $ a = 4 $:

Order $ a = 5 $:

1. What is Diffraction Grating Calculator?

Definition: This calculator computes the diffraction angles ($ \theta_a $) for different orders of a diffraction grating, which splits light into its component wavelengths based on interference.

Purpose: It is used in optics to determine the angles at which light of a specific wavelength will diffract, useful in spectroscopy and optical experiments.

2. How Does the Calculator Work?

The calculator uses the diffraction grating equation:

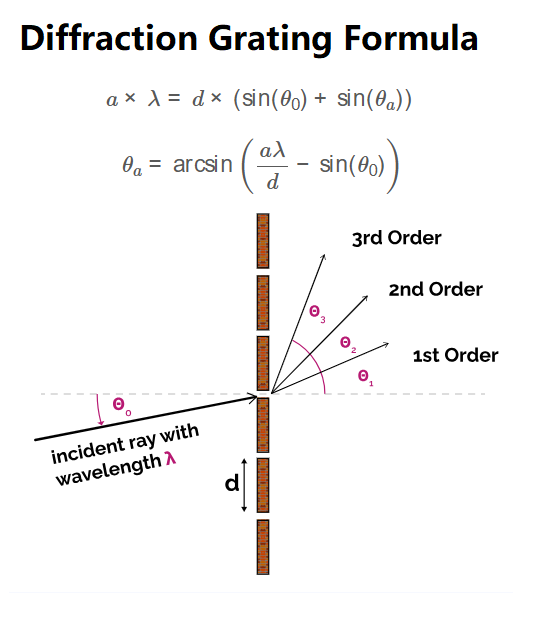
Formula: \[ a \times \lambda = d \times (\sin(\theta_0) + \sin(\theta_a)) \] Rearranged to solve for $ \theta_a $: \[ \theta_a = \arcsin\left(\frac{a \lambda}{d} - \sin(\theta_0)\right) \] Where:

$ \lambda $: Wavelength of the incident ray (m, mm, μm, nm, pm, Å)
$ d $: Grating spacing (m, mm, μm, nm, pm, Å)
$ \theta_0 $: Angle of incidence (rad, deg)
$ \theta_a $: Diffraction angle for order $ a $ (rad, deg)
$ a $: Order of the diffracted image (positive integer, e.g., 1, 2, 3, ...)

Unit Conversions:

Wavelength ($ \lambda $) and Grating Spacing ($ d $): m, mm (1 mm = $ 10^{-3} $ m), μm (1 μm = $ 10^{-6} $ m), nm (1 nm = $ 10^{-9} $ m), pm (1 pm = $ 10^{-12} $ m), Å (1 Å = $ 10^{-10} $ m)
Angles ($ \theta_0 $, $ \theta_a $): rad, deg (1 deg = $ \frac{\pi}{180} $ rad)
Grating Density: lines/mm (converted to $ d $ in meters by $ d = \frac{1}{\text{density} \times 1000} $)

Steps:

Enter the wavelength ($ \lambda $), grating density (lines/mm), angle of incidence ($ \theta_0 $), and maximum order to calculate.
Convert $ \lambda $ to meters and compute $ d $ from the grating density.
Convert $ \theta_0 $ to radians.
For each order $ a $, calculate $ \sin(\theta_a) = \frac{a \lambda}{d} - \sin(\theta_0) $.
Compute $ \theta_a = \arcsin\left(\frac{a \lambda}{d} - \sin(\theta_0)\right) $.
Convert each $ \theta_a $ to the selected unit (rad or deg).
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Diffraction Grating Calculation

Calculating diffraction angles is crucial for:

Spectroscopy: Separating light into its component wavelengths to analyze the spectrum of a light source.
Optics: Designing optical instruments like spectrometers and monochromators.
Education: Understanding the principles of wave interference and diffraction in physics.

4. Using the Calculator

Examples:

Example 1: For $ \lambda = 500 \, \text{nm} $, grating density = 1000 lines/mm, $ \theta_0 = 30^\circ $, max order = 3, angles in degrees:
- Convert: $ \lambda = 500 \times 10^{-9} \, \text{m} $, $ d = \frac{1}{1000 \times 1000} = 10^{-6} \, \text{m} $, $ \theta_0 = 30 \times \frac{\pi}{180} = 0.5236 \, \text{rad} $
- $ \sin(\theta_0) = 0.5 $
- Order 1: $ \sin(\theta_1) = \frac{1 \times 500 \times 10^{-9}}{10^{-6}} - 0.5 = 0.5 - 0.5 = 0 $, $ \theta_1 = 0 \, \text{rad} \approx 0^\circ $
- Order 2: $ \sin(\theta_2) = \frac{2 \times 500 \times 10^{-9}}{10^{-6}} - 0.5 = 1 - 0.5 = 0.5 $, $ \theta_2 = \arcsin(0.5) \approx 0.5236 \, \text{rad} \approx 30^\circ $
- Order 3: $ \sin(\theta_3) = \frac{3 \times 500 \times 10^{-9}}{10^{-6}} - 0.5 = 1.5 - 0.5 = 1 $, $ \theta_3 = \arcsin(1) \approx 90^\circ $
Example 2: For $ \lambda = 600 \, \text{nm} $, grating density = 500 lines/mm, $ \theta_0 = 0^\circ $, max order = 2, angles in radians:
- Convert: $ \lambda = 600 \times 10^{-9} \, \text{m} $, $ d = \frac{1}{500 \times 1000} = 2 \times 10^{-6} \, \text{m} $, $ \theta_0 = 0 \, \text{rad} $
- $ \sin(\theta_0) = 0 $
- Order 1: $ \sin(\theta_1) = \frac{1 \times 600 \times 10^{-9}}{2 \times 10^{-6}} - 0 = 0.3 $, $ \theta_1 = \arcsin(0.3) \approx 0.3047 \, \text{rad} $
- Order 2: $ \sin(\theta_2) = \frac{2 \times 600 \times 10^{-9}}{2 \times 10^{-6}} - 0 = 0.6 $, $ \theta_2 = \arcsin(0.6) \approx 0.6435 \, \text{rad} $

5. Frequently Asked Questions (FAQ)

Q: What is a diffraction grating?
A: A diffraction grating is an optical component with a periodic structure that splits light into its component wavelengths by interference, producing diffracted images at specific angles.

Q: Why might a diffraction angle not be possible for a given order?
A: If $ \sin(\theta_a) $ is not between -1 and 1, the diffraction angle is not physically possible for that order, as it exceeds the range of real angles.

Q: How do I determine the grating spacing $ d $?
A: The grating spacing $ d $ is the inverse of the grating density (lines per unit length). For example, a density of 1000 lines/mm means $ d = \frac{1}{1000} \, \text{mm} = 10^{-6} \, \text{m} $.