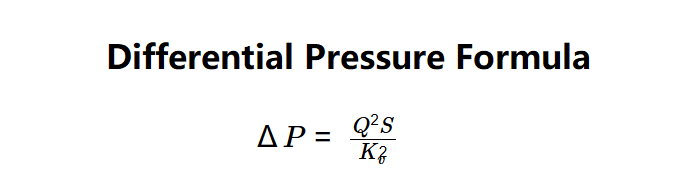Differential Pressure Calculator

Flow Factor (\( K_v \)):

Specific Gravity Input Method:

Select Fluid:

Volumetric Flow Rate (\( Q \)):

1. What is Differential Pressure Calculator?

Definition: This calculator computes the differential pressure (\( \Delta P \)) across a valve or restriction in a pipe, based on the flow factor, specific gravity of the fluid, and volumetric flow rate.

Purpose: It is used in fluid dynamics and engineering to determine the pressure drop caused by a valve or restriction, aiding in the design and analysis of piping systems, such as in HVAC, water treatment, and industrial processes.

2. How Does the Calculator Work?

The calculator uses the following formula:

\( \Delta P = \frac{Q^2 S}{K_v^2} \)

Where:

\( K_v \): Flow factor (m³/h);
\( S \): Specific gravity of the fluid (dimensionless, relative to water at 4°C);
\( Q \): Volumetric flow rate (m³/h in the formula, converted from input units);
\( \Delta P \): Differential pressure (bar).

Steps:

Enter the flow factor (\( K_v \)) with its unit.
Choose the specific gravity (\( S \)) by selecting a fluid or entering a custom value.
Enter the volumetric flow rate (\( Q \)) with its unit.
Convert \( K_v \) and \( Q \) to base units (m³/h for both).
Calculate the differential pressure: \( \Delta P = \frac{Q^2 S}{K_v^2} \).
Convert the differential pressure to the selected output unit and display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 5 decimal places.

3. Importance of Differential Pressure Calculation

Calculating the differential pressure is crucial for:

Valve Sizing: Determining the pressure drop across a valve to ensure it can handle the required flow rate without excessive energy loss.
System Efficiency: Optimizing the design of piping systems to minimize pressure losses and ensure efficient fluid transport.
Performance Analysis: Evaluating the performance of flow control devices in various applications, such as in industrial processes, water distribution, and HVAC systems.

4. Using the Calculator

Example 1 (Predefined Fluid): Calculate \( \Delta P \) for water flowing through a valve with the following properties:

Flow Factor: \( K_v = 10 \, \text{m}^3/\text{h} \);
Fluid: Water (at 15.6°C, \( S = 1.00 \));
Volumetric Flow Rate: \( Q = 0.1 \, \text{m}^3/\text{s} \);
Convert \( Q \): \( Q = 0.1 \times 3600 = 360 \, \text{m}^3/\text{h} \);
Differential Pressure: \( \Delta P = \frac{(360)^2 \times 1.00}{(10)^2} = 1296 \, \text{bar} \);
Result: \( \Delta P = 1296.00000 \, \text{bar} \).

Example 2 (Custom Specific Gravity, Different Units): Calculate \( \Delta P \) with the following properties:

Flow Factor: \( K_v = 5 \, \text{l/min} \);
Specific Gravity: \( S = 0.8 \);
Volumetric Flow Rate: \( Q = 100 \, \text{l/min} \);
Convert \( K_v \): \( K_v = 5 \times 0.06 = 0.3 \, \text{m}^3/\text{h} \);
Convert \( Q \): \( Q = 100 \times 0.06 = 6 \, \text{m}^3/\text{h} \);
Differential Pressure: \( \Delta P = \frac{(6)^2 \times 0.8}{(0.3)^2} = 320 \, \text{bar} \);
Result (in kPa): \( \Delta P = 32000.00000 \, \text{kPa} \).

5. Frequently Asked Questions (FAQ)

Q: What does the flow factor \( K_v \) represent?
A: The flow factor (\( K_v \)) is a measure of the flow capacity of a valve, indicating the flow rate (in m³/h) of water at 20°C that will pass through the valve with a 1 bar pressure drop.

Q: Why does the differential pressure depend on specific gravity?
A: The specific gravity (\( S \)) adjusts the pressure drop for fluids other than water, accounting for differences in density that affect the flow characteristics through the valve.

Q: Can this calculator be used for gases?
A: This calculator is designed for liquids using the given formula. For gases, a different approach is typically required, often involving compressibility factors and a different flow coefficient (\( C_v \)).