Differential Microstrip Impedance from Z0 Calculator

Single-Ended Impedance (\( Z_0 \)):

Substrate Height (\( h \)):

Distance Between Traces (\( d \)):

1. What is a Differential Microstrip Impedance from Z0 Calculator?

Definition: This calculator determines the differential impedance \( Z_d \) of a differential microstrip transmission line based on the single-ended impedance \( Z_0 \), substrate height (\( h \)), and the distance between the traces (\( d \)).

Purpose: It helps RF and PCB designers calculate the differential impedance for high-speed digital and RF circuits when the single-ended impedance is known, ensuring signal integrity and minimizing reflections.

2. How Does the Calculator Work?

The calculator uses the following formula to compute the differential impedance:

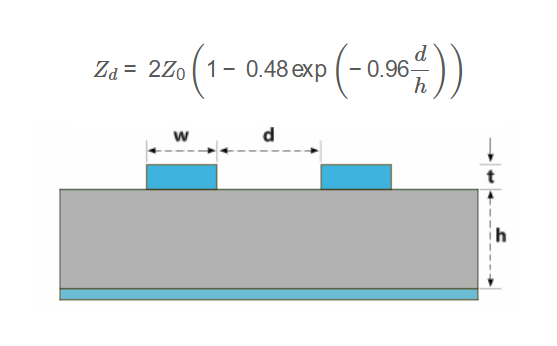
Differential Impedance \( Z_d \): \[ Z_d = 2 Z_0 \left( 1 - 0.48 \exp\left( -0.96 \frac{d}{h} \right) \right) \]

Where:

\( Z_d \): Differential impedance in ohms
\( Z_0 \): Single-ended impedance in ohms
\( h \): Substrate height (distance to ground plane)
\( d \): Distance between the two traces

Unit Conversions:

Input Impedance (\( Z_0 \)):
1 ohm = 1000 mΩ
Input Dimensions (\( h, d \)):
1 mm = 39.3701 mils
1 μm = 0.0393701 mils
Output Impedance (\( Z_d \)):
1 ohm = 1000 mΩ

Steps:

Enter the single-ended impedance \( Z_0 \) and select the unit (ohms or mΩ).
Enter the substrate height \( h \) and the distance between traces \( d \), selecting the unit for each (mils, mm, or μm).
Click "Calculate" to compute \( Z_d \).
The result is initially displayed in ohms.
Select a different unit for \( Z_d \) (ohms or mΩ) from the dropdown after the result to convert the displayed value.

3. Importance of Differential Microstrip Impedance Calculation

Calculating the differential impedance of a microstrip is crucial for:

Signal Integrity: Ensures minimal distortion and crosstalk in high-speed differential signals.
Impedance Matching: Reduces reflections by matching the differential impedance to the system requirements.
Design Optimization: Allows designers to adjust trace spacing and substrate height to achieve the desired impedance.

4. Using the Calculator

Examples:

Example 1: \( Z_0 = 100 \) ohms, \( h = 30 \) mils, \( d = 20 \) mils, Result in ohms
- Ratio: \( \frac{d}{h} = \frac{20}{30} \approx 0.667 \)
- Exp term: \( \exp(-0.96 \times 0.667) \approx 0.527 \)
- \( Z_d = 2 \times 100 \times (1 - 0.48 \times 0.527) \approx 149.37 \, \text{ohms} \)
Example 2: \( Z_0 = 100000 \) mΩ, \( h = 0.762 \) mm, \( d = 508 \) μm, Result in mΩ
- Convert: \( Z_0 = 100000 \div 1000 = 100 \, \text{ohms} \), \( h = 0.762 \times 39.3701 \approx 30 \, \text{mils} \), \( d = 508 \times 0.0393701 \approx 20 \, \text{mils} \)
- Same as Example 1: \( Z_d \approx 149.37 \, \text{ohms} \)
- Result in mΩ: \( Z_d = 149.37 \times 1000 = 149370 \, \text{mΩ} \)
Example 3: \( Z_0 = 90 \) ohms, \( h = 762 \) μm, \( d = 0.508 \) mm, Result in ohms
- Convert: \( h = 762 \times 0.0393701 \approx 30 \, \text{mils} \), \( d = 0.508 \times 39.3701 \approx 20 \, \text{mils} \)
- Ratio and exp term same as above: \( \exp(-0.96 \times 0.667) \approx 0.527 \)
- \( Z_d = 2 \times 90 \times (1 - 0.48 \times 0.527) \approx 134.43 \, \text{ohms} \)

5. Frequently Asked Questions (FAQ)

Q: What is a differential microstrip?
A: A differential microstrip is a pair of parallel conductive traces on a dielectric substrate over a ground plane, used to transmit differential signals in high-speed digital and RF circuits.

Q: How does \( Z_d \) relate to \( Z_0 \)?
A: \( Z_d \) (differential impedance) accounts for the coupling between the two traces, typically being less than \( 2 \times Z_0 \) due to the proximity of the traces, as captured by the exponential term in the formula.

Q: What factors affect the accuracy of this calculation?
A: The formula assumes ideal conditions. Real-world factors like frequency-dependent effects, dielectric variations, and manufacturing tolerances can affect accuracy. For precise designs, use field solvers or consult PCB manufacturers.