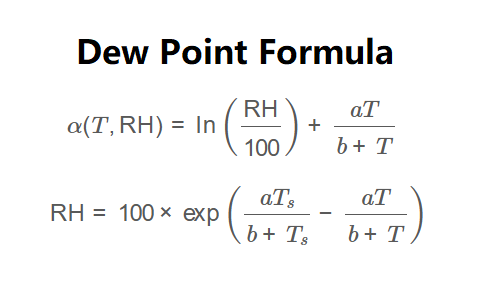Dew Point Calculator

Air Temperature:

Input Type:

Relative Humidity (\( \text{RH} \)): %

1. What is the Dew Point Calculator?

Definition: This calculator computes the dew point temperature (\( T_s \)) given the air temperature and relative humidity, or calculates the relative humidity (\( \text{RH} \)) given the air temperature and dew point temperature, using the Magnus-Tetens formula. The dew point is the temperature at which air becomes saturated, leading to condensation.

Purpose: It is used in meteorology, HVAC design, and environmental science to assess moisture levels in the air, predict condensation, and ensure comfort or safety in various applications.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ \alpha(T, \text{RH}) = \ln\left(\frac{\text{RH}}{100}\right) + \frac{a T}{b + T} \] \[ T_s = \frac{b \times \alpha(T, \text{RH})}{a - \alpha(T, \text{RH})} \] If calculating relative humidity: \[ \text{RH} = 100 \times \exp\left( \frac{a T_s}{b + T_s} - \frac{a T}{b + T} \right) \] where:

\( T_s \): Dew point temperature (°C, °F, K)
\( T \): Air temperature (°C, °F, K)
\( \text{RH} \): Relative humidity (%)
\( a \): Magnus coefficient, 17.625
\( b \): Magnus coefficient, 243.04 °C

Unit Conversions:

Temperature (Air Temperature, Dew Point):
- 1 °C = 1 °C
- 1 °F = (T - 32) × 5/9 °C
- 1 K = T - 273.15 °C
- For output: 1 °C = T × 9/5 + 32 °F, 1 °C = T + 273.15 K

Steps:

Enter the air temperature in °C, °F, or K (default is 25°C, step size 0.00001).
Select the input type (relative humidity or dew point).
If using relative humidity, enter the relative humidity as a percentage (default is 50%, step size 0.00001); if using dew point, enter the dew point in °C, °F, or K (default is 15°C, step size 0.00001).
Convert temperature and dew point (if provided) to Celsius (°C).
Calculate the dew point using the Magnus-Tetens formula if relative humidity is provided, or calculate the relative humidity if the dew point is provided.
Convert the dew point to the selected temperature unit (if calculated), and display the result, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.

3. Importance of Dew Point and Relative Humidity Calculation

Calculating dew point and relative humidity is crucial for:

Meteorology: Predicting weather conditions such as fog, dew, or frost formation, and assessing the likelihood of precipitation.
HVAC Systems: Ensuring optimal indoor humidity levels for comfort and preventing mold growth by controlling condensation.
Aviation: Assessing the risk of icing on aircraft surfaces, as the dew point indicates the temperature at which condensation occurs.

4. Using the Calculator

Examples:

Example 1: Calculate the dew point with a temperature of 25°C and relative humidity of 50%, with dew point in °C:
- Enter Temperature = 25 °C.
- Enter Relative Humidity = 50%.
- Calculate \( \alpha \): \( \alpha(25, 50) = \ln(50/100) + \frac{17.625 \times 25}{243.04 + 25} = -0.6931 + 1.6426 = 0.9495 \).
- Calculate dew point: \( T_s = \frac{243.04 \times 0.9495}{17.625 - 0.9495} = \frac{230.7718}{16.6755} = 13.8381 \, \text{°C} \).
- Result: \( T_s = 13.8381 \, \text{°C} \).
Example 2: Calculate the relative humidity with a temperature of 86°F and dew point of 59°F:
- Enter Temperature = 86 °F, convert to °C: \( (86 - 32) \times 5/9 = 30 \, \text{°C} \).
- Enter Dew Point = 59 °F, convert to °C: \( (59 - 32) \times 5/9 = 15 \, \text{°C} \).
- Calculate RH: \( \text{RH} = 100 \times \exp\left( \frac{17.625 \times 15}{243.04 + 15} - \frac{17.625 \times 30}{243.04 + 30} \right) = 100 \times \exp(1.0249 - 1.9346) = 100 \times \exp(-0.9097) = 100 \times 0.4027 = 40.27\% \).
- Result: \( \text{RH} = 40.2700\% \).

5. Frequently Asked Questions (FAQ)

Q: What is the dew point?
A: The dew point is the temperature at which air becomes saturated, and water vapor begins to condense into liquid water, forming dew, fog, or clouds. It indicates the moisture content of the air.

Q: Why use the Magnus-Tetens formula?
A: The Magnus-Tetens formula provides a relatively simple and accurate approximation for dew point and relative humidity calculations within the temperature range of -40°C to 50°C, with an uncertainty of about 0.35°C, making it suitable for practical applications.

Q: How does relative humidity relate to dew point?
A: Relative humidity is the ratio of the actual vapor pressure to the saturation vapor pressure at a given temperature, expressed as a percentage. The dew point is the temperature at which the current vapor pressure equals the saturation vapor pressure, so a smaller difference between temperature and dew point indicates higher relative humidity.